题目内容
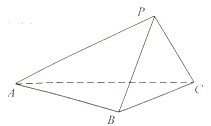
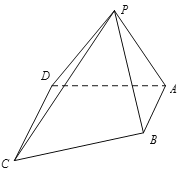
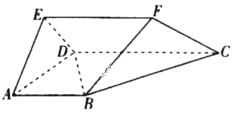
【题目】如图,已知多面体![]() 中,
中,![]() 、
、![]() 均为正三角形,平面
均为正三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求该多面体的体积.
,求该多面体的体积.
【答案】(1)见解析(2)![]()
【解析】
试题(1)通过解三角形以及勾股定理得![]() . 取
. 取![]() 的中点
的中点![]() ,则
,则![]() 再由面面垂直性质定理得
再由面面垂直性质定理得![]() 平面
平面![]() ,即得
,即得![]() ,取
,取![]() 的中点
的中点![]() ,根据平行四边形性质得
,根据平行四边形性质得![]() ,即
,即![]() ,最后根据线面垂直判定定理得
,最后根据线面垂直判定定理得![]() 平面
平面![]() ;(2)通过割补法将多面体转化为一个三棱柱,再由面面垂直性质定理得
;(2)通过割补法将多面体转化为一个三棱柱,再由面面垂直性质定理得![]() 平面
平面![]() ,利用补形法得一个四棱柱体积的一半,最后代入柱体体积公式求体积.
,利用补形法得一个四棱柱体积的一半,最后代入柱体体积公式求体积.
试题解析:解:(Ⅰ)因为![]() ,所以
,所以![]() ,
,![]() 为正三角形,所以
为正三角形,所以![]() .
.
设![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
在![]() 中,由余弦定理,得
中,由余弦定理,得
![]() ,
,
所以![]() ,所以
,所以![]() .
.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,因为
,因为![]() 为正三角形,所以
为正三角形,所以![]() ,
,
因为平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() ,且
,且![]() ,所以四边形
,所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
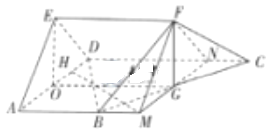
(Ⅱ)过![]() 作直线
作直线![]() ,延长
,延长![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() .
.
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() 且
且![]() ,所以四边形
,所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
同理![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() ,所以
,所以![]() ,所以多面体
,所以多面体![]() 为三棱柱.
为三棱柱.
过![]() 作
作![]() 于
于![]() 点,因为平面
点,因为平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以线段![]() 的长即三棱柱
的长即三棱柱![]() 的高,在
的高,在![]() 中,
中,![]() ,
,
所以三棱柱![]() 的体积为
的体积为![]() .
.
因为三棱锥![]() 与
与![]() 的体积相等,所以所求多面体的体积为
的体积相等,所以所求多面体的体积为![]() .
.

练习册系列答案
相关题目
【题目】某商场周年庆,准备提供一笔资金,对消费满一定金额的顾客以参与活动的方式进行奖励.顾客从一个装有大小相同的2个红球和4个黄球的袋中按指定规则取出2个球,根据取到的红球数确定奖励金额,具体金额设置如下表:
取到的红球数 | 0 | 1 | 2 |
奖励(单位:元) | 5 | 10 | 50 |
现有两种取球规则的方案:
方案一:一次性随机取出2个球;
方案二:依次有放回取出2个球.
(Ⅰ)比较两种方案下,一次抽奖获得50元奖金概率的大小;
(Ⅱ)为使得尽可能多的人参与活动,作为公司的负责,你会选择哪种方案?请说明理由.