题目内容
空间四边形ABCD的一组对边BC、AD的长分别为6、4，且夹角为60°，则连接对角线AC、BD中点的线段长为（ ）
分析：设AC、BD的中点分别为E、F，取AB的中点G，连接EG、GF，由题设知EGF为BC、AD的夹角，再由余弦定理能求出连接对角线AC、BD中点的线段长．
解答：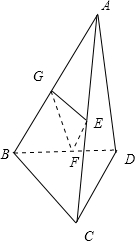
解：设AC、BD的中点分别为E、F，取AB的中点G，连接EG、GF，
∵空间四边形ABCD的一组对边BC、AD的长分别为6、4，且夹角为60°，
∴GE∥BC，GE=
=3，
GF∥AD，GF=
=2，
∴∠EGF为BC、AD的夹角，∴∠EGF=60°
∴EF2=GE2+GF2-2GE•GFcos∠EGF
=9+4-2×3×2×
=7，
∴EF=
．
故选A．
解：设AC、BD的中点分别为E、F，取AB的中点G，连接EG、GF，∵空间四边形ABCD的一组对边BC、AD的长分别为6、4，且夹角为60°，
∴GE∥BC，GE=
| BC |
| 2 |
GF∥AD，GF=
| AD |
| 2 |
∴∠EGF为BC、AD的夹角，∴∠EGF=60°
∴EF2=GE2+GF2-2GE•GFcos∠EGF
=9+4-2×3×2×
| 1 |
| 2 |
∴EF=
| 7 |
故选A．
点评：本题考查空间中点、线、面间的距离计算，解题时要认真审题，仔细解答，注意等价转化思想的合理运用．
练习册系列答案
相关题目
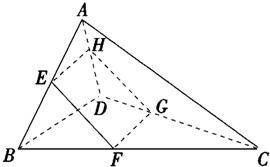空间四边形ABCD的两条对棱AC、BD的长分别为5和4，则平行于两条对棱的截面四边形EFGH在平移过程中，周长的取值范围是
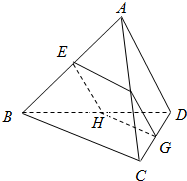空间四边形ABCD的对棱AD，BC成60°的角，且AD=BC=a，平行于AD与BC的截面分别交AB，AC，CD，BD于E、F、G、H．
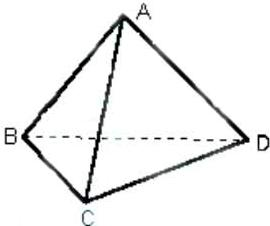如图，一空间四边形ABCD的对边AB与CD，AD与BC都互相垂直，用向量证明：AC与BD也互相垂直．