题目内容
设函数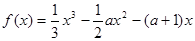
①当a=1时,求函数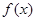 的极值;
的极值;
②若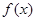 在
在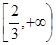 上是递增函数,求实数a的取值范围;
上是递增函数,求实数a的取值范围;
③当0<a<2时, ,求
,求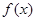 在该区间上的最小值.
在该区间上的最小值.
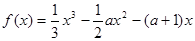
①当a=1时,求函数
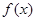 的极值;
的极值;②若
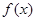 在
在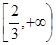 上是递增函数,求实数a的取值范围;
上是递增函数,求实数a的取值范围;③当0<a<2时,
 ,求
,求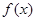 在该区间上的最小值.
在该区间上的最小值.(1)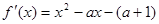 ;(2)
;(2)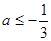 ;(3)当x=2时取得最小值,为
;(3)当x=2时取得最小值,为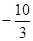 .
.
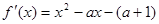 ;(2)
;(2)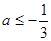 ;(3)当x=2时取得最小值,为
;(3)当x=2时取得最小值,为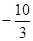 .
.(1)求出导数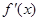 ,然后根据
,然后根据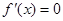 解出极值点,进而根据极值的确定方法求极值即可.
解出极值点,进而根据极值的确定方法求极值即可.
(2)由题意知把此问题转化为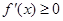 在
在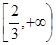 上恒成立问题解决即可,
上恒成立问题解决即可,
(3)令 得,
得,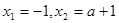 ,由于0<a<2,所以当x=1或4时
,由于0<a<2,所以当x=1或4时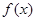 有可能取最大值,然后再分类讨论可求出a值.再进一步确定最小值.
有可能取最大值,然后再分类讨论可求出a值.再进一步确定最小值.
解:因为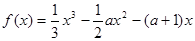
所以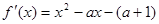 …………………………………………1分
…………………………………………1分
① 因为a=1,所以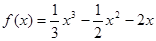
所以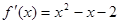 …………………………………………2分
…………………………………………2分
令 得,
得,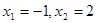 …………………………………………3分
…………………………………………3分
列表如下:
当x=-1时取得极大值,为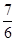 ;
;
当x=2时取得极小值,为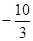 …………………………………………5分
…………………………………………5分
② 因为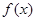 在
在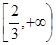 上是递增函数,
上是递增函数,
所以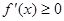 在
在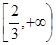 上恒成立,…………………………………………6分
上恒成立,…………………………………………6分
即 在
在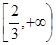 上恒成立.
上恒成立.
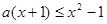
解得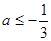 …………………………………………8分
…………………………………………8分
③令 得,
得,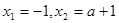
列表如下:
由上表知当x=1或4时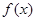 有可能取最大值,………………………………9分
有可能取最大值,………………………………9分
令 解得a=-4不符合题意舍.…………………………………………10分
解得a=-4不符合题意舍.…………………………………………10分
令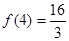 解得a=1…………………………………………11分
解得a=1…………………………………………11分
因为a=1,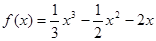
所以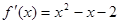
令 得,
得,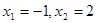 …………………………………………12分
…………………………………………12分
列表如下:
当x=2时取得最小值,为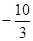 …………………………………………14分
…………………………………………14分
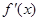 ,然后根据
,然后根据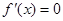 解出极值点,进而根据极值的确定方法求极值即可.
解出极值点,进而根据极值的确定方法求极值即可.(2)由题意知把此问题转化为
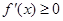 在
在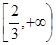 上恒成立问题解决即可,
上恒成立问题解决即可,(3)令
 得,
得,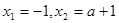 ,由于0<a<2,所以当x=1或4时
,由于0<a<2,所以当x=1或4时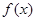 有可能取最大值,然后再分类讨论可求出a值.再进一步确定最小值.
有可能取最大值,然后再分类讨论可求出a值.再进一步确定最小值.解:因为
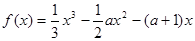
所以
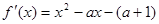 …………………………………………1分
…………………………………………1分① 因为a=1,所以
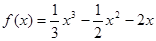
所以
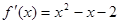 …………………………………………2分
…………………………………………2分令
 得,
得,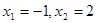 …………………………………………3分
…………………………………………3分列表如下:
| x | 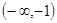 | -1 | 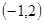 | 2 | 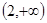 |
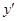 | + | 0 | - | 0 | + |
| y | 增 | 极大值 | 减 | 极小值 | 增 |
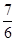 ;
;当x=2时取得极小值,为
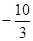 …………………………………………5分
…………………………………………5分② 因为
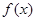 在
在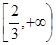 上是递增函数,
上是递增函数,所以
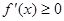 在
在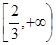 上恒成立,…………………………………………6分
上恒成立,…………………………………………6分即
 在
在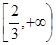 上恒成立.
上恒成立.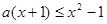
解得
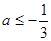 …………………………………………8分
…………………………………………8分③令
 得,
得,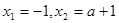
列表如下:
| x | 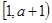 |  |  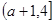 |
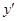 | - | 0 | + |
| y | 减 | 极小值 | 增 |
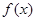 有可能取最大值,………………………………9分
有可能取最大值,………………………………9分令
 解得a=-4不符合题意舍.…………………………………………10分
解得a=-4不符合题意舍.…………………………………………10分令
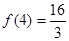 解得a=1…………………………………………11分
解得a=1…………………………………………11分因为a=1,
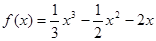
所以
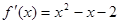
令
 得,
得,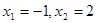 …………………………………………12分
…………………………………………12分列表如下:
| x | 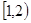 | 2 | 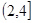 |
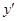 | - | 0 | + |
| y | 减 | 极小值 | 增 |
当x=2时取得最小值,为
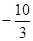 …………………………………………14分
…………………………………………14分
练习册系列答案
相关题目
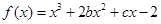 的图象在与
的图象在与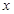 轴交点处的切线方程是
轴交点处的切线方程是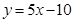 .则函数
.则函数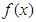 的解析式为__________。
的解析式为__________。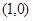 的直线与曲线
的直线与曲线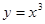 和
和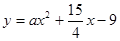 都相切,则
都相切,则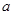 =_____.
=_____.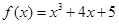 的图像在
的图像在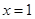 处的切线在x轴上的截距为( )
处的切线在x轴上的截距为( )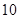
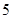
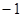
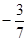
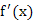 ,若函数
,若函数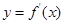 的图象关于直线
的图象关于直线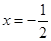 对称,且
对称,且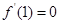 .](Ⅰ)求实数
.](Ⅰ)求实数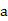 ,
,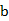 的值;(5分)(Ⅱ)求函数
的值;(5分)(Ⅱ)求函数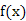 的极值
的极值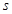 (单位:m)关于时间
(单位:m)关于时间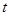 (单位:s)的函数为
(单位:s)的函数为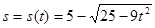 ,求当
,求当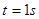 时,梯子上端下滑的速度为( )
时,梯子上端下滑的速度为( )



 的单调递减区间为 .
的单调递减区间为 .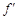 (-1)=4,则a的值等于________.
(-1)=4,则a的值等于________.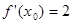 ,则
,则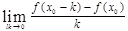 的值为( )
的值为( )