题目内容
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分
已知函数 .
.
(1)若 为偶函数,求
为偶函数,求 的值;
的值;
(2)若 在区间
在区间 上是增函数,试求
上是增函数,试求 、
、 应满足的条件.
应满足的条件.
 (2)
(2) 且
且 .
.
【解析】
试题分析:(1)若函数是偶函数则
 的关系,(2)对于含有绝对值号的函数的单调性的有关题目,先去绝对值号(注意一定要明确自变量的取值范围,选择与之对应的对应关系),写成分段函数,然后再逐段进行讨论。
的关系,(2)对于含有绝对值号的函数的单调性的有关题目,先去绝对值号(注意一定要明确自变量的取值范围,选择与之对应的对应关系),写成分段函数,然后再逐段进行讨论。
试题解析:(1)
 为偶函数,∴对任意的
为偶函数,∴对任意的 ,都有
,都有 , 2分
, 2分
即
 4分
4分
得  。 6分
。 6分
(2)记 , 8分
, 8分
①当 时,
时, 在区间
在区间 上是增函数,即
上是增函数,即 在区间
在区间 上是增函数,
上是增函数,
∴ ,
, 10分
10分
②当 时,
时, 在区间
在区间 上是增函数,即
上是增函数,即 在区间
在区间 上是减函数但
上是减函数但 在区间
在区间 上是增函数,故不可能 12分
上是增函数,故不可能 12分
∴ 在区间
在区间 上是增函数时,
上是增函数时, 、
、 应满足的条件为
应满足的条件为 且
且 14分
14分
考点:函数的单调性及奇偶性.

练习册系列答案
相关题目
 (
( ,
, ,
, )的部分图象如图所示,则
)的部分图象如图所示,则 ( )
( )
 B.
B. C.
C. D.
D.
 在点
在点 处的切线方程为
处的切线方程为 ,则
,则
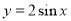 的定义域为
的定义域为 ,值域为
,值域为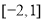 ,则
,则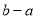 的值不可能是( )
的值不可能是( )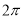 B.
B.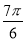 C.
C. D.
D.
 的定义域为
的定义域为 ,
, 的定义域为
的定义域为 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
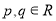 ,则“
,则“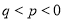 ”是“
”是“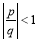 ”的
”的  .
.
 是定义在
是定义在 上的偶函数,对任意
上的偶函数,对任意 ,都有
,都有 ,且当
,且当 时,
时, .若函数
.若函数 在区间
在区间 恰有3个不同的零点,则
恰有3个不同的零点,则 的取值范围是 .
的取值范围是 .