题目内容
9.已知向量$\overrightarrow{a}$=(sinα,$\frac{3}{2}$),$\overrightarrow{b}$=(cosα,-1),且$\overrightarrow{a}$∥$\overrightarrow{b}$(1)若α为第二象限角,求$\frac{sin(-α-\frac{π}{2})cos(\frac{3}{2}π+α)tan(π-α)}{tan(-α-π)sin(-π-α)}$的值;
(2)求cos2α-sin2α的值.
分析 (1)通过向量的共线求出正切函数值,利用诱导公式化简已知条件然后求解即可.
(2)化简表达式为正切函数的形式,然后求解即可.
解答 解:向量$\overrightarrow{a}$=(sinα,$\frac{3}{2}$),$\overrightarrow{b}$=(cosα,-1),且$\overrightarrow{a}$∥$\overrightarrow{b}$,
可得-sinα=$\frac{3}{2}$cosα,可得tanα=-$\frac{3}{2}$,
(1)$\frac{sin(-α-\frac{π}{2})cos(\frac{3}{2}π+α)tan(π-α)}{tan(-α-π)sin(-π-α)}$=$\frac{cosαsinαtanα}{tanαsinα}$=-cosα=-$\sqrt{\frac{1}{1+ta{n}^{2}α}}$=-$\sqrt{\frac{1}{1+\frac{9}{4}}}$=-$\frac{2\sqrt{13}}{13}$.
(2)cos2α-sin2α=$\frac{co{s}^{2}α-2sinαcosα}{co{s}^{2}α+si{n}^{2}α}$=$\frac{1-2tanα}{1+ta{n}^{2}α}$=$\frac{1-2×(-\frac{3}{2})}{1+\frac{9}{4}}$=$\frac{16}{13}$.
点评 本题考查诱导公式以及向量的共线,三角函数的化简求值,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.定义在区间(0,$\frac{π}{2}$)上的函数y=6cosx与y=5tanx的图象交点为P,过点P作x轴的垂线,垂足为P1,直线PP1与y=sinx的图象交于点P2,则线段P1P2的长度为( )
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{7}}{4}$ |
14.若三角形ABC为钝角三角形,三边为2,3,x,则x的取值范围是( )
| A. | (1,$\sqrt{5}$) | B. | (1,$\sqrt{5}$)∪($\sqrt{13}$,5) | C. | ($\sqrt{5}$,$\sqrt{13}$) | D. | ($\sqrt{13}$,5) |
19.cos(-$\frac{26π}{3}$)的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
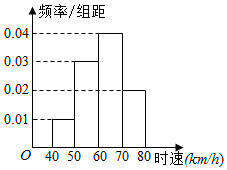 关于统计数据的分析,有以下几个结论:
关于统计数据的分析,有以下几个结论: