题目内容
16.正三棱柱ABC-A1B1C1侧面的三条对角线AB1,BC1,CA1中,若A1C⊥AB1,求证:AB1⊥BC1.分析 取AC的中点O,A1C1的中点D,连接OD,以O为原点,分别以OC,OB,OD为x,y,z轴正方向建立空间直角坐标系,设AB=1,AA1=x,则可得:$\overrightarrow{{A}_{1}C}$=(1,0,-x),$\overrightarrow{A{B}_{1}}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,x),$\overrightarrow{B{C}_{1}}$=($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,x),由A1C⊥AB1,解得:x=$\frac{\sqrt{2}}{2}$,可证$\overrightarrow{A{B}_{1}}$•$\overrightarrow{B{C}_{1}}$=0,从而证明AB1⊥BC1.
解答  证明:如图,取AC的中点O,A1C1的中点D,连接OD,以O为原点,分别以OC,OB,OD为x,y,z轴正方向建立空间直角坐标系,设AB=1,AA1=x,则可得:A(-$\frac{1}{2}$,0,0),C($\frac{1}{2}$,0,0),
证明:如图,取AC的中点O,A1C1的中点D,连接OD,以O为原点,分别以OC,OB,OD为x,y,z轴正方向建立空间直角坐标系,设AB=1,AA1=x,则可得:A(-$\frac{1}{2}$,0,0),C($\frac{1}{2}$,0,0),
B(0,$\frac{\sqrt{3}}{2}$,0),A1(-$\frac{1}{2}$,0,x),C1($\frac{1}{2}$,0,x),
B1(0,$\frac{\sqrt{3}}{2}$,x),
∴可得:$\overrightarrow{{A}_{1}C}$=(1,0,-x),$\overrightarrow{A{B}_{1}}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,x),
$\overrightarrow{B{C}_{1}}$=($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,x).
∵A1C⊥AB1,
∴$\frac{1}{2}$-x2=0,解得:x=$\frac{\sqrt{2}}{2}$,
∴$\overrightarrow{A{B}_{1}}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{2}}{2}$),$\overrightarrow{B{C}_{1}}$=($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{2}}{2}$).
∵$\overrightarrow{A{B}_{1}}$•$\overrightarrow{B{C}_{1}}$=$\frac{1}{2}×\frac{1}{2}+\frac{\sqrt{3}}{2}×(-\frac{\sqrt{3}}{2})+\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}$=0,
∴AB1⊥BC1.得证.
点评 本题主要考查了线面垂直的性质和判定,同时考查了空间想象能力、运算求解的能力、以及转化与划归的思想,属于中档题.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案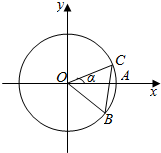 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | -$\frac{5}{13}$ | D. | -$\frac{12}{13}$ |
| A. | -$\frac{1}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
| A. | {1,5} | B. | {1,2,5} | C. | {2,3} | D. | {1,2,3,5} |