题目内容
点![]() 是抛物线
是抛物线![]() 上的不同两点,过
上的不同两点,过![]() 分别作抛物线
分别作抛物线![]() 的切线,两条切线交于点
的切线,两条切线交于点![]() 。
。
(1)求证:![]() 是
是![]() 与
与![]() 的等差中项;
的等差中项;
(2)若直线![]() 过定点
过定点![]() ,求证:原点
,求证:原点![]() 是
是![]() 的垂心;
的垂心;
(3)在(2)的条件下,求![]() 的重心
的重心![]() 的轨迹方程。
的轨迹方程。
(1)证明见解析。
(2)证明见解析。
(3)![]()
解析:
(1)对![]() 求导 得
求导 得![]() ,
,
所以直线![]() ,即
,即![]()
同理, 直线![]() , 解得
, 解得 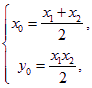
所以![]() 是
是![]() 与
与![]() 的等差中项; (5分)
的等差中项; (5分)
(2)设直线![]() ,代入
,代入![]() 整理得
整理得![]() .
.
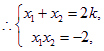 ,得
,得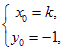
![]() 即
即![]() ;
;
![]() ,
, ![]()
![]() ,
,
![]() , 同理
, 同理![]() ,
,
所以原点![]() 是
是![]() 的垂心; (10分,只需证明
的垂心; (10分,只需证明![]() 两个垂直就得满分)
两个垂直就得满分)
(3)设![]() 的重心
的重心![]() ,则
,则
![]() ,
,
![]()
因为![]() ,所以点
,所以点![]() 的轨迹方程为
的轨迹方程为![]() . (15分)
. (15分)

练习册系列答案
相关题目
 的斜率为
的斜率为 且过点
且过点 ,抛物线
,抛物线
 , 直线与抛物线
, 直线与抛物线 是抛物线的焦点,点
是抛物线的焦点,点 为抛物线内一定点,点
为抛物线内一定点,点 为抛物线上一动点.
为抛物线上一动点. 的最小值;
的最小值; 为坐标原点,问是否存在点
为坐标原点,问是否存在点 ,使过点
,使过点 两点,且以
两点,且以 为直径的圆恰过坐标原点, 若存在,求出动点
为直径的圆恰过坐标原点, 若存在,求出动点 是抛物线
是抛物线 上的不同两点,过
上的不同两点,过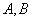 分别作
分别作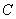 的切线,两条切线交于点
的切线,两条切线交于点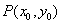 .
.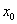 是
是 与
与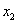 的等差中项;
的等差中项;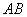 过定点
过定点 ,求证:原点
,求证:原点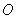 是
是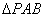 的垂心;
的垂心;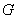 的轨迹方程.
的轨迹方程.