题目内容
已知数列{an}满足a1=1,a2=- ,从第二项起,{an}是以
,从第二项起,{an}是以 为公比的等比数列,{an}的前n项和为Sn,试问:S1,S2,S3…,Sn,…能否构成等比数列?为什么?
为公比的等比数列,{an}的前n项和为Sn,试问:S1,S2,S3…,Sn,…能否构成等比数列?为什么?
当n 2时,an=a2qn-2=-
2时,an=a2qn-2=- (
( )n-2=-(
)n-2=-( )n-1 ∴an=
)n-1 ∴an=

当n=1时,S1=a1=1
当n 2时,Sn=a1+a2+…+an=1-
2时,Sn=a1+a2+…+an=1- -(
-( )2-…-(
)2-…-( )n-1=1-[
)n-1=1-[ +(
+( )2+…+(
)2+…+( )n-1]=1-
)n-1]=1-

∴Sn=( )n-1
)n-1 

 {Sn}可以构成等比数列。
{Sn}可以构成等比数列。

练习册系列答案
相关题目
 ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是 ,得到黄球或绿球的概率是
,得到黄球或绿球的概率是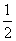 ,试求得到黑球、黄球、绿球的概率各是多少?
,试求得到黑球、黄球、绿球的概率各是多少?
 求
求 .
. ,则
,则 .
. 如图1,
如图1, 、
、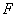 分别是正方体
分别是正方体 中
中 、
、 上的动点(不含端点),则四边形
上的动点(不含端点),则四边形 的俯视图可能是
的俯视图可能是