题目内容
△ABC中，AB=2，AC=3，BC=4，则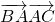
=
- A.
- B.
- C.
- D.
D
分析：△ABC中，由余弦定理求出cosA=-
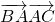，利用两个向量的数量积的定义，求得的值．
解答：△ABC中，由余弦定理可得 16=4+9-2×2×3cosA，∴cosA=-．
∴=|
|•|
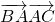|cos（π-A）=2×3（-cosA）=，
故选：D．
点评：本题主要考查两个向量的数量积的定义，余弦定理的应用，属于基础题，求出cosA=-，是解题的关键，注意
的夹角等于π-A，这是解题的易错点．
分析：△ABC中，由余弦定理求出cosA=-
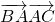，利用两个向量的数量积的定义，求得的值．解答：△ABC中，由余弦定理可得 16=4+9-2×2×3cosA，∴cosA=-
．∴
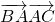=||•||cos（π-A）=2×3（-cosA）=，故选：D．
点评：本题主要考查两个向量的数量积的定义，余弦定理的应用，属于基础题，求出cosA=-
，是解题的关键，注意的夹角等于π-A，这是解题的易错点． 
练习册系列答案
相关题目
如图，A，B，C，D为空间四点．在△ABC中，AB=2，AC=BC=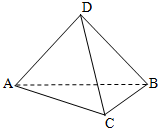
如图，A、B、C、D是空间四点，在△ABC中，AB=2，AC=BC=