题目内容
已知a1,a2,…,an都是正数，且a1+a2+…+an＝1，求证：(a1+
)2+(a2+
)2+…+(an+
)2≥
.
证明:原不等式等价于
n［(a1+)2+(a2+)2+…+(an+)2］≥(n2+1)2.
∵(12+12+…+12)·［(a1+)2+(a2+
)2+…+(an+
)2］≥［(a1+
)+(a2+
)+…+(an+
)］2
=［1+(
+
+…+
)］2,①
又由调和平均数≤算术平均数知
,
∴
+
+…+
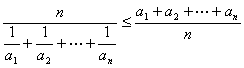≥n2，代入①式即得.
练习册系列答案
轻松暑假总复习系列答案
相关题目