题目内容

（理科做）等比数列{an}中，已知a1+a2+a3=8，a1+a2+…+a6=7，记Sn=a1+a2+…+an，则
limn→∞
Sn=
 
．
分析：由题意：“a1+a2+a3=8，a4+a5+a6=-1”知a1=
32
3
，q=-
1
2
，根据
lim
n→∞
Sn=
a1
1-q
 即可求得结果．
解答：解：设等比数列{an}的公比为q，
则a1+a2+a3+…+a6=a1+a2+a3+q3（a1+a2+a3）=（1+q3）（a1+a2+a3）=8•（1+q3）=7，
解得q=-
1
2
，a1+a2+a3=a1-
1
2
a1+
1
4
a1=8
解得a1=
32
3
．
∴
lim
n→∞
Sn=
a1
1-q
=
32
3
1+
1
2
=
64
9
．
故答案为：
64
9
．
点评：本题考查等比数列的计算和极限，解题时要正确选取公式，注意公式的灵活运用，属中档题．
练习册系列答案
相关题目
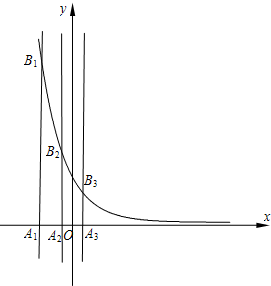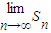（2006•蚌埠二模）已知等差数列{an}的首项为p，公差为d（d＞0）．对于不同的自然数n，直线x=an与x轴和指数函数f(x)=(
12
)x的图象分别交于点An与Bn（如图所示），记Bn的坐标为（an，bn），直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2，一般地记直角梯形AnAn+1Bn+1Bn的面积为sn．
（1）求证数列{sn}是公比绝对值小于1的等比数列；
（2）设{an}的公差d=1，是否存在这样的正整数n，构成以bn，bn+1，bn+2为边长的三角形？并请说明理由；
（3）（理科做，文科不做）设{an}的公差d=1，是否存在这样的实数p使得（1）中无穷等比数列{sn}各项的和S＞2010？如果存在，给出一个符合条件的p值；如果不存在，请说明理由．（参考数据：210=1024）
（理科做）等比数列{an}中，已知a1+a2+a3=8，a1+a2+…+a6=7，记Sn=a1+a2+…+an，则
lim
n→∞
Sn=______．

(理科做)设等比数列的前项和，首项，公比.

(1)若数列满足，，求数列的通项公式；

(2)若，记，数列的前项和为，求证：当时，
（理科做）等比数列{an}中，已知a1+a2+a3=8，a1+a2+…+a6=7，记Sn=a1+a2+…+an，则=    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网