Question

某单位投资生产A产品时，每生产1百吨需要资金2百万元，需场地2百平方米，可获利润3百万元；投资生产B产品时，每生产1百吨需要资金3百万元，需场地1百平方米，可获利润2百万元．现该单位有可使用资金14百万元，场地9百平方米，如果利用这些资金和场地用来生产A、B两种产品，那么分别生产A、B两种产品各多少时，可获得最大利润？最大利润是多少？

Answer 1

分析：由投资生产A产品时，每生产1百吨需要资金2百万元，需场地2百平方米，可获利润3百万元；投资生产B产品时，每生产1百米需要资金3百万元，需场地1百平方米，可获利润2百万元．现该单位有可使用资金14百万元，场地9百平方米，我们设生产A产品x百吨，生产B产品y百米，共获得利润S百万元，我们可以得到满足条件的约束条件和目标函数，然后利用线性规划来解答即可得到答案．

解答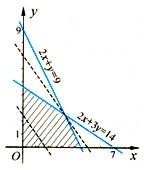：解：设生产A产品x百吨，生产B产品y百米，共获得利润S百万元，（1分）
则

2x+3y≤14 2x+y≤9 x≥0 y≥0

（5分）
目标函数为S=3x+2y，
作出可行域如图（6分）
由

2x+y=9 2x+3y=14

解得直线与2x+y=9和2x+3y=14的交点为(

13

4

，

5

2

)（7分）
平移直线y=-

3

2

x+

S

2

，当它经过直线与2x+y=9和2x+3y=14的交点(

13

4

，

5

2

)时，
直线y=-

3

2

x+

S

2

在y轴上截距

S

2

最大，S也最大． （9分）
此时，S=3×

13

4

+2×

5

2

=14.75． （10分）
因此，生产A产品3.25百吨，生产B产品2.5百米，可获得最大利润，最大利润为1475万元． （12分）

点评：本题考查的知识点是简单线性规划的应用，根据已知条件的限制条件，构造出约束条件和目标函数是解答此类问题的关键．