题目内容
已知(a2+1)n展开式中各项系数之和等于( x2+
x2+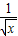 )5的展开式的常数项,而(a2+1)n的展开式的二项式系数最大的项的系数等于54,求a的值.
)5的展开式的常数项,而(a2+1)n的展开式的二项式系数最大的项的系数等于54,求a的值.
【答案】分析:由二项式定理通项公式知Tr+1=C5r( x2)5-r(
x2)5-r( )r=(
)r=( )5-r•C5r•x
)5-r•C5r•x .由20-5r=0,知r=4,由题意得2n=16,n=4.再由二项式系数的性质知,(a2+1)n展开式中二项式系数最大的项是中间项T3,由此可求出a的值.
.由20-5r=0,知r=4,由题意得2n=16,n=4.再由二项式系数的性质知,(a2+1)n展开式中二项式系数最大的项是中间项T3,由此可求出a的值.
解答:解:由( x2+
x2+ )5得,
)5得,
Tr+1=C5r( x2)5-r(
x2)5-r( )r=(
)r=( )5-r•C5r•x
)5-r•C5r•x .
.
令Tr+1为常数项,则20-5r=0,
∴r=4,∴常数项T5=C54× =16.
=16.
又(a2+1)n展开式的各项系数之和等于2n.
由题意得2n=16,∴n=4.
由二项式系数的性质知,(a2+1)n展开式中二项式系数最大的项是中间项T3,
∴C42a4=54,
∴a=± .
.
点评:本题考查二项式定理的应用和二项式系数的性质,解题时要注意根据实际情况灵活地运用公式.
 x2)5-r(
x2)5-r( )r=(
)r=( )5-r•C5r•x
)5-r•C5r•x .由20-5r=0,知r=4,由题意得2n=16,n=4.再由二项式系数的性质知,(a2+1)n展开式中二项式系数最大的项是中间项T3,由此可求出a的值.
.由20-5r=0,知r=4,由题意得2n=16,n=4.再由二项式系数的性质知,(a2+1)n展开式中二项式系数最大的项是中间项T3,由此可求出a的值.解答:解:由(
 x2+
x2+ )5得,
)5得,Tr+1=C5r(
 x2)5-r(
x2)5-r( )r=(
)r=( )5-r•C5r•x
)5-r•C5r•x .
.令Tr+1为常数项,则20-5r=0,
∴r=4,∴常数项T5=C54×
 =16.
=16.又(a2+1)n展开式的各项系数之和等于2n.
由题意得2n=16,∴n=4.
由二项式系数的性质知,(a2+1)n展开式中二项式系数最大的项是中间项T3,
∴C42a4=54,
∴a=±
 .
.点评:本题考查二项式定理的应用和二项式系数的性质,解题时要注意根据实际情况灵活地运用公式.

练习册系列答案
相关题目
 x2+
x2+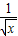 )5的展开式的常数项,而(a2+1)n的展开式的二项式系数最大的项的系数等于54,求a的值.
)5的展开式的常数项,而(a2+1)n的展开式的二项式系数最大的项的系数等于54,求a的值.