题目内容
如数列{an}的前n项和为Sn=2an+1，则数列{an}的通项公式为
-2n-1
-2n-1
．分析：由Sn=2an+1和Sn+1=2an+1+1相减得an+1=2an+1-2an，所以
=2，由此可求出数列{an}的通项公式．
| an+1 |
| an |
解答：解：由Sn=2an+1，
得Sn+1=2an+1+1，
二式相减得：an+1=2an+1-2an，
∴
=2，
∴数列{an}是公比为2的等比数列，
又∵S1=2a1+1，
∴a1=-1，
∴an=-2n-1．
故答案为：-2n-1．
得Sn+1=2an+1+1，
二式相减得：an+1=2an+1-2an，
∴
| an+1 |
| an |
∴数列{an}是公比为2的等比数列，
又∵S1=2a1+1，
∴a1=-1，
∴an=-2n-1．
故答案为：-2n-1．
点评：本题考查数列的通项公式的求法，解题时要认真审题，注意相减法和递推公式的灵活运用．
练习册系列答案
相关题目
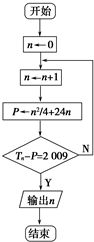数列{an}的前n项和为Sn，已知Sn=
如图，第一个图是正三角形，将此正三角形的每条边三等分，以中间一段为边向外作正三角形，并擦去中间一段，得第2个图，将第2个图中的每一条边三等分，以中间一段为边向外作正三角形，并擦去中间一段，得第3个图，如此重复操作至第n个图，用an表示第n个图形的边数，则数列an的前n项和Sn等于