题目内容
 如图,第一个图是正三角形,将此正三角形的每条边三等分,以中间一段为边向外作正三角形,并擦去中间一段,得第2个图,将第2个图中的每一条边三等分,以中间一段为边向外作正三角形,并擦去中间一段,得第3个图,如此重复操作至第n个图,用an表示第n个图形的边数,则数列an的前n项和Sn等于
如图,第一个图是正三角形,将此正三角形的每条边三等分,以中间一段为边向外作正三角形,并擦去中间一段,得第2个图,将第2个图中的每一条边三等分,以中间一段为边向外作正三角形,并擦去中间一段,得第3个图,如此重复操作至第n个图,用an表示第n个图形的边数,则数列an的前n项和Sn等于分析:根据图形得到,a1=3,a2=12,a3=48,由题意知:每一条边经一次变化后总变成四条边,即
=4(n>2),由等比数列的定义知:an=3×4n-1,于是根据等比数列前n项和公式即可求解
| an |
| an-1 |
解答:解:∵a1=3,a2=12,a3=48
由题意知:每一条边经一次变化后总变成四条边,即
=4(n>2),
由等比数列的定义知:an=3×4n-1
∴Sn=
=4n-1
故答案为:4n-1
由题意知:每一条边经一次变化后总变成四条边,即
| an |
| an-1 |
由等比数列的定义知:an=3×4n-1
∴Sn=
| 3×(1-4n) |
| 1-4 |
故答案为:4n-1
点评:本题考查了等比数列的前n项和,还考查对图形的阅读能力,属于基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
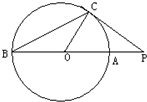 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)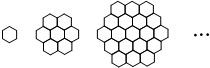 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.
 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=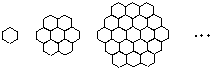 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图2为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(n)=
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图2为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(n)=