题目内容
在几何体ABCDE中,∠BAC=
(1)设平面ABE与平面ACD的交线为直线l,求证:l∥平面BCDE;
(2)设F是BC的中点,求证:平面AFD⊥平面AFE;
(3)求几何体ABCDE的体积.
解:(1)证明:∵CD⊥平面ABC,BF⊥平面ABC,
∴CD∥BE.∴CD∥平面ABE.
又l=平面ACD∩平面ABE,
∴CD∥l.
又l![]() 平面BCDE,CD
平面BCDE,CD![]() 平面BCDE,
平面BCDE,
∴l∥平面BCDE.
(2)证明:在△DEF中,FD=![]() ,FE=
,FE=![]() ,DE=3,
,DE=3,

∴FD⊥FE.
∵CD⊥平面ABC,∴CD⊥AF.又BC⊥AF,∴AF⊥平面BCDE.
∴AF⊥FD.∴FD⊥平面AFE.又FD![]() 平面AFD,∴平面AFD⊥平面AFE.
平面AFD,∴平面AFD⊥平面AFE.
(3)VABCDE=VA—BCDE
=![]() S四边形BCDE·AF
S四边形BCDE·AF
=![]() ×
×![]() (1+2)×2
(1+2)×2![]() ×
×![]()
=2.

练习册系列答案
相关题目
 如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点.
如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点. 在几何体ABCDE中,∠BAC=
在几何体ABCDE中,∠BAC=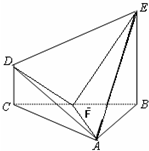 在几何体ABCDE中,
在几何体ABCDE中, 在几何体ABCDE中,∠BAC=
在几何体ABCDE中,∠BAC=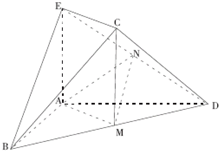 (2013•合肥二模)如图,在几何体ABCDE中,AB=AD=2,AB丄AD,AD丄平面ABE.M为线段BD的中点,MC∥AE,AE=MC=
(2013•合肥二模)如图,在几何体ABCDE中,AB=AD=2,AB丄AD,AD丄平面ABE.M为线段BD的中点,MC∥AE,AE=MC=