题目内容
(12分)如图,已知三棱柱ABC—A1B1C1中,底面ABC是等边三角形,侧棱与底面垂直,点E,F分别为棱BB1,AC中点。
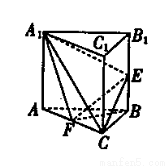
(1)证明:BF//平面A1CE;
(2)若AA1=6,AC=4,求直线CE与平面A1EF所成角的正弦值。
(1)证明见解析;(2) .
.
【解析】
试题分析:(1)用线面平行的判断定理,证明BF//EG,而BF 平面A1CE,EG
平面A1CE,EG 平面A1CE,∴BF//平面A1CE.
平面A1CE,∴BF//平面A1CE.
(2)以A为原点,AB的垂线,AB及AA1所在直线分别为x轴,y轴z轴建立直角坐标系A-xyz,

则 ,设平面A1EF的一个法向量为
,设平面A1EF的一个法向量为 ,解得n=(7
,解得n=(7 ,3,4),
,3,4),
则 .
.
试题解析:(1)取A1C中点G,连接FG,EG,
则FG//FG,且FG= AA1.
AA1.
又由三棱柱的定义及E为BB1中点可得EB//AA1,且EB= AA1,
AA1,
∴EB//FG,且EB=FG,∴四边形BFGE为平行四边形,
∴BF//EG,而BF 平面A1CE,EG
平面A1CE,EG 平面A1CE,
平面A1CE,
∴BF//平面A1CE.
(2)如图,以A为原点,AB的垂线,AB及AA1所在直线分别为x轴,y轴,z轴建立直角坐标系A-xyz
则 ,设平面A1EF的一个法向量为
,设平面A1EF的一个法向量为 ,
,
由条件可得 , 即
, 即 ,
,
令y=3可得n=(7 ,3,4),
,3,4),
设直线CE与平面A1EF所成角为θ,
则 .
.
考点:线面平行的判断定理,直线与平面所成的角.
考点分析: 考点1:点、线、面之间的位置关系 考点2:异面直线所成的角 考点3:线面所成的角 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 若
若 与
与 平行,则实数
平行,则实数 的值是
的值是 的部分图象如图所示,则
的部分图象如图所示,则 的解析式是( )
的解析式是( )
 B.
B.
 D.
D.
 =10,则
=10,则 等于( )
等于( )
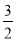 B.0 C.1 D.0或-
B.0 C.1 D.0或-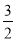
 是定义在R上且周期为2的函数,在区间
是定义在R上且周期为2的函数,在区间 ,上,
,上,
 ,若
,若 ,则
,则 _______.
_______. 是等比数列,命题
是等比数列,命题 “若公比
“若公比 ,则数列
,则数列 ,则
,则 .
.