题目内容
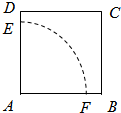 如图,设边长为1的正方形纸片,以A为圆心,AE=a(0<a≤1)为半径画圆弧EF,裁剪的扇形AEF围成一个圆锥的侧面,余下的部分裁剪出它的底面.当圆锥的侧面积最大时,圆锥底面的半径r=
如图,设边长为1的正方形纸片,以A为圆心,AE=a(0<a≤1)为半径画圆弧EF,裁剪的扇形AEF围成一个圆锥的侧面,余下的部分裁剪出它的底面.当圆锥的侧面积最大时,圆锥底面的半径r=分析:根据题意,在正方形余下部分裁剪出圆锥底面,当底面圆与BC、CD和弧EF都相切时圆锥的侧面积可达最大值.由此利用直线与圆、圆与圆的位置关系,算出底面圆半径r满足
=a+(1+
)r,化简可得围成的圆锥侧面积关于r的二次函数表达式.由扇形与圆M能围成圆锥解出0<r≤
,利用二次函数的单调性加以计算,可得当圆锥的侧面积最大时,圆锥底面的半径r的值.
| 2 |
| 2 |
5
| ||
| 23 |
解答:解: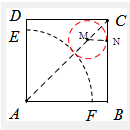 根据题意,欲在正方形ABCD内且在扇形AEF外的余下部分裁剪出圆锥的底面,
根据题意,欲在正方形ABCD内且在扇形AEF外的余下部分裁剪出圆锥的底面,
则圆锥的底面圆与BC、CD和弧EF都相切,设此时圆的圆心为M,与BC边相切于点N.
设圆锥底面圆的半径是r,由两圆外切的性质可得AM=a+r,
又∵Rt△CMN中,∠NCM=45°,
∴CM=
CN=
r,可得AC=AM+CM=a+(1+
)r.
∵AC为边长为1的正方形的对角线,得AC=
,
∴
=a+(1+
)r,
可得a=
-(1+
)r…(*)
又∵若要能使扇形AEF与圆M围成圆锥,则必须弧EF长大于或等于圆M的周长,
∴
a≥2πr,即a≥4r,代入(*)可得(5+
)r≤
,
解得0<r≤
.
∵围成的圆锥母线为a,底面圆半径为r,
∴围成圆锥的侧面积S侧=πar=πr[
-(1+
)r],
可得S侧为关于r的二次函数,在区间(0,
]上为关于r的增函数,
∴当r=
时,S侧有最大值.
综上所述,可得圆锥的侧面积最大时,圆锥底面的半径r=
.
故答案为:
 根据题意,欲在正方形ABCD内且在扇形AEF外的余下部分裁剪出圆锥的底面,
根据题意,欲在正方形ABCD内且在扇形AEF外的余下部分裁剪出圆锥的底面,则圆锥的底面圆与BC、CD和弧EF都相切,设此时圆的圆心为M,与BC边相切于点N.
设圆锥底面圆的半径是r,由两圆外切的性质可得AM=a+r,
又∵Rt△CMN中,∠NCM=45°,
∴CM=
| 2 |
| 2 |
| 2 |
∵AC为边长为1的正方形的对角线,得AC=
| 2 |
∴
| 2 |
| 2 |
可得a=
| 2 |
| 2 |
又∵若要能使扇形AEF与圆M围成圆锥,则必须弧EF长大于或等于圆M的周长,
∴
| π |
| 2 |
| 2 |
| 2 |
解得0<r≤
5
| ||
| 23 |
∵围成的圆锥母线为a,底面圆半径为r,
∴围成圆锥的侧面积S侧=πar=πr[
| 2 |
| 2 |
可得S侧为关于r的二次函数,在区间(0,
5
| ||
| 23 |
∴当r=
5
| ||
| 23 |
综上所述,可得圆锥的侧面积最大时,圆锥底面的半径r=
5
| ||
| 23 |
故答案为:
5
| ||
| 23 |
点评:本题将一个边长为1有正方形裁剪,再围成一个圆锥,求圆锥的侧面积最大时的半径长.着重考查了圆锥的侧面积公式、直线与圆和圆与圆的位置关系、二次函数的单调性及其应用等知识,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
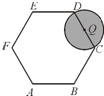 如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量
如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量| AP |
| AB |
| AF |
| A、(1,2] |
| B、[5,6] |
| C、[2,5] |
| D、[3,5] |
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和) (2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量
(2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量
 (2)当
(2)当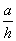 为多少时,体积V最大,最大值是多少?
为多少时,体积V最大,最大值是多少?