题目内容
18．在平面直角坐标系中，方程|x|+|y|=4所表示的曲线是以（0，4），（4，0），（0，-4），（-4，0）为顶点的正方形．分析 去掉绝对值，可得方程|x|+|y|=4的曲线围成的封闭图形．
解答 解：x≥0，y≥0方程为x+y=4；x≥0，y≤0方程为x-y=4；x≤0，y≥0方程为-x+y=4；x≤0，y≤0方程为-x-y=4，
∴方程|x|+|y|=4的曲线围成的封闭图形是一个以（0，4），（4，0），（0，-4），（-4，0）为顶点的正方形，
故答案为：以（0，4），（4，0），（0，-4），（-4，0）为顶点的正方形．
点评 本题考查的知识点是曲线与方程，分析出几何体的形状是解答的关键，难度中档．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
8．根据上海高考改革方案，2017年，高中生可从思想政治、历史、地理、物理、化学、生命科学6门学业考试科目中选3门参加等级性考试，并且这3门学业考试科目等级考试成绩将这算，计入高考总分，上海37所本科高校，从目前公布的1096个专业（类）的选考科目老看，学生选考物理可以满足1070个专业选科要求，覆盖率97.63%；选考化学可以满足992个专业选科要求，覆盖率为90.51%；选考生命科学可以满足877个专业选科要求，覆盖率为80.02%，地理、历史、思想政治的覆盖率分别为64.05%、63.5%、62.14%，为了进一步调查学生选考的意向，某机构对本市两所学校各100名高一新生进行了选考调查，且规定从6门学业考试中每一位学生只能选择1门，结果如下：
（1）分别计算甲乙两校选考理科专业的频率，若将该频率视为概率，求从乙校高一新生中随机选取3人，其中恰有2人选考理科专业的概率；
（2）若从甲校高一新生中任取1人，从乙校高一新生中任取2人，记3人中选考理科专业的人数为随机变量X，求X的分布列和数学期望．
| 物理 | 化学 | 生命科学 | 政治 | 历史 | 地理 | |
| 甲校 | 35 | 20 | 15 | 7 | 8 | 15 |
| 乙校 | 30 | 14 | 16 | 11 | 14 | 15 |
（2）若从甲校高一新生中任取1人，从乙校高一新生中任取2人，记3人中选考理科专业的人数为随机变量X，求X的分布列和数学期望．
6．
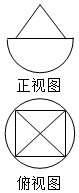一个半球与一个正四棱锥组成的几何体的正视图与俯视图如图所示，其中正视图中的等腰三角形的腰长为$\sqrt{3}$．若正四棱锥的顶点均在该半球所在球的球面上，则此球的半径为（ ）
一个半球与一个正四棱锥组成的几何体的正视图与俯视图如图所示，其中正视图中的等腰三角形的腰长为$\sqrt{3}$．若正四棱锥的顶点均在该半球所在球的球面上，则此球的半径为（ ）| A． | 2 | B． | $\frac{3}{2}$$\sqrt{2}$ | C． | $\frac{12}{5}$$\sqrt{5}$ | D． | $\sqrt{6}$ |