题目内容
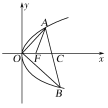
【题目】设![]() 为抛物线
为抛物线![]() 的焦点,过点
的焦点,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)若![]() ,求此时直线
,求此时直线![]() 的方程;
的方程;
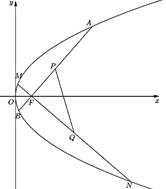
(2)若与直线![]() 垂直的直线
垂直的直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 相交于点
相交于点![]() 、
、![]() ,设线段
,设线段![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() ,如图,求证:直线
,如图,求证:直线![]() 过定点;
过定点;
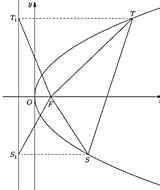
(3)设抛物线![]() 上的点
上的点![]() 、
、![]() 在其准线上的射影分别为
在其准线上的射影分别为![]() 、
、![]() ,若△
,若△![]() 的面积是△
的面积是△![]() 的面积的两倍,如图,求线段
的面积的两倍,如图,求线段![]() 中点的轨迹方程.
中点的轨迹方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)求出抛物线的焦点坐标,由直线方程的点斜式写出直线l的方程,和抛物线方程联立后利用![]() 2
2![]() 得直线
得直线![]() 方程.
方程.
(2由(1)得点P![]() ,又直线
,又直线![]() 与直线
与直线![]() 垂直,将m换为
垂直,将m换为![]() ,同理可得Q(
,同理可得Q(![]() ,﹣
,﹣![]() ).由此可求直线PQ的方程,可得结论;
).由此可求直线PQ的方程,可得结论;
(3)利用△![]() 的面积是△
的面积是△![]() 的面积的两倍,求出N的坐标,再利用直线的斜率公式及点差法求TS中点的轨迹方程.
的面积的两倍,求出N的坐标,再利用直线的斜率公式及点差法求TS中点的轨迹方程.
(1)抛物线焦点坐标为F(1,0),设直线![]() 方程为x=my+1,
方程为x=my+1,
设点A(x1,y1),B(x2,y2),
联立![]() ,得:y2﹣4my﹣4=0,
,得:y2﹣4my﹣4=0,
则由韦达定理有:y1+y2=4m,①,y1y2=﹣4,②
∵![]() 2
2![]() ,
,
∴1﹣x1=2(x2﹣1),﹣y1=2y2,③,
由①②③可得m2![]() ,∴
,∴![]() ,
,
∴直线方程为x=![]() y+1,即
y+1,即![]() .
.
(2)由(1)得点P![]() ,又直线
,又直线![]() 与直线
与直线![]() 垂直,将m换为
垂直,将m换为![]() ,
,
同理可得Q(![]() ,﹣
,﹣![]() ).
).
m![]() 时,直线PQ的斜率kPQ
时,直线PQ的斜率kPQ ,
,
直线PQ的方程为:y-2m![]() (x﹣1﹣2
(x﹣1﹣2![]() ),整理为m(x﹣3)﹣(m2﹣1)y=0,于是直线PQ恒过定点E(3,0),
),整理为m(x﹣3)﹣(m2﹣1)y=0,于是直线PQ恒过定点E(3,0),
m=±1时,直线PQ的方程为:x=3,也经过点E(3,0).
综上所述:直线PQ恒过定点E(3,0).
(3)设S(x1,y1),T(x2,y2),

F(1,0),准线为 x=﹣1,![]() 2|
2|![]() |=|y1﹣y2|,
|=|y1﹣y2|,
设直线TS与x轴交点为N,
∴S△TSF![]() |FN||y1﹣y2|,
|FN||y1﹣y2|,
∵![]() 的面积是△TSF的面积的两倍,
的面积是△TSF的面积的两倍,
∴![]() |FN|=
|FN|=![]() ,∴|FN|=1,
,∴|FN|=1,
∴xN=2,即N(2,0).
设TS中点为M(x,y),由 得
得![]() ﹣
﹣![]() =4(x1﹣x2),
=4(x1﹣x2),
又![]() ,
,
∴![]() ,即y2=2x﹣4.
,即y2=2x﹣4.
∴TS中点轨迹方程为y2=2x﹣4.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.