题目内容
函数y=x2+|x-a|+b在区间(-∞,0]上为减函数,则a的取值范围是
- A.a≥0
- B.a≤0
- C.a≥1
- D.a≤1
A
分析:先去掉绝对值将函数转化为分段函数 然后每一段按照条件分析单调性,得到结果,两者取并集.
然后每一段按照条件分析单调性,得到结果,两者取并集.
解答:
∵y=x2+x-a+b的对称轴为x=- ,
,
且在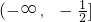 上单调递减,在
上单调递减,在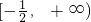 上单调递增
上单调递增
所以必有a≥0
∵y=x2-x+a+b的对称轴为 ,
,
且在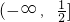 上单调递减,在
上单调递减,在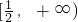 上单调递增
上单调递增
所以必有a≥0
综上:a≥0
故选A
点评:本题主要考查函数的转化与函数的性质,绝对值函数往往转化为分段函数,是高考常类型,属中档题.
分析:先去掉绝对值将函数转化为分段函数
 然后每一段按照条件分析单调性,得到结果,两者取并集.
然后每一段按照条件分析单调性,得到结果,两者取并集.解答:

∵y=x2+x-a+b的对称轴为x=-
 ,
,且在
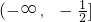 上单调递减,在
上单调递减,在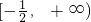 上单调递增
上单调递增所以必有a≥0
∵y=x2-x+a+b的对称轴为
 ,
,且在
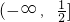 上单调递减,在
上单调递减,在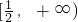 上单调递增
上单调递增所以必有a≥0
综上:a≥0
故选A
点评:本题主要考查函数的转化与函数的性质,绝对值函数往往转化为分段函数,是高考常类型,属中档题.

练习册系列答案
相关题目