题目内容
函数y=| x2-x+n |
| x2+1 |
| a | n |
| 1 |
| 2 |
(1)求数列{cn}的通项公式;
(2)若数列{dn}是等差数列,且dn=
| Sn |
| n+c |
(3)若f(n)=
| dn |
| (n+36)dn+1 |
分析:(1)根据题中已知条件便可求出anbn,然后代入cn的表达式中即可求出数列{cn}的通项公式;
(2)由(1)中cn的通项公式先求出Sn的表达式,然后根据题意求出dn的通项公式,再根据dn为等差数列的条件便可求出c的值;
(3)将(2)中求得的dn 的通项公式代入求出f(n)的表达式,然后根据不等式的性质可知当n=6时,f(n)有最大值.
(2)由(1)中cn的通项公式先求出Sn的表达式,然后根据题意求出dn的通项公式,再根据dn为等差数列的条件便可求出c的值;
(3)将(2)中求得的dn 的通项公式代入求出f(n)的表达式,然后根据不等式的性质可知当n=6时,f(n)有最大值.
解答:解:(1)由y=
,(n∈N*,y≠1),得x2(y-1)+x+y-n=0
∵x∈R,y≠1,
∴△=1-4(y-1)(y-n)≥0,即4y2-4(1+n)y+4n-1≤0
由题意知:an,bn是方程4y2-4(1+n)y+4n-1=0的两根,
(2)Sn=2n2-n,dn=
,
∴d1=
,d2=
,d3=
∵{dn}为等差数列,
∴2d2=d1+d3,
∴2c2+c=0,
∴c=-
或c=0(舍)
经检验c=
时,{dn}是等差数列,dn=2n;
(3)f(n)=
=
≤
=
| x2-x+n |
| x2+1 |
∵x∈R,y≠1,
∴△=1-4(y-1)(y-n)≥0,即4y2-4(1+n)y+4n-1≤0
由题意知:an,bn是方程4y2-4(1+n)y+4n-1=0的两根,
|
(2)Sn=2n2-n,dn=
| 2n2-n |
| n+c |
∴d1=
| 1 |
| 1+c |
| 6 |
| 2+c |
| 15 |
| 3+c |
∵{dn}为等差数列,
∴2d2=d1+d3,
∴2c2+c=0,
∴c=-
| 1 |
| 2 |
经检验c=
| 1 |
| 2 |
(3)f(n)=
| 2n |
| (n+36)(2n+2) |
| 1 | ||
n+
|
| 1 | ||
37+2
|
| 1 |
| 49 |
|
点评:本题主要考查了等差数列、等比数列的基本公式以及数列与函数的综合运用,考查了学生的计算能力和对数列的综合掌握,解题时注意整体思想和转化思想的运用,属于中档题.

练习册系列答案
相关题目
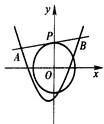 设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于A,B两点,点O是坐标原点.
设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于A,B两点,点O是坐标原点.