题目内容
x,y∈(0,+∞),x+2y=1,则 的最小值是________.
的最小值是________.
3+2
分析:由x+2y=1? =(
=( )•(x+2y)=1+
)•(x+2y)=1+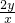 +
+ +2,结合条件,应用基本不等式即可.
+2,结合条件,应用基本不等式即可.
解答:∵x,y∈(0,+∞),x+2y=1,
∴ =(
=( )•(x+2y)=1+
)•(x+2y)=1+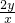 +
+ +2≥3+2
+2≥3+2 (当且仅当
(当且仅当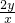 =
= ,即x=
,即x= -1时取“=”).
-1时取“=”).
故答案为:3+2 .
.
点评:本题考查基本不等式,着重考查代入法及基本不等式的应用,属于基础题.

分析:由x+2y=1?
 =(
=( )•(x+2y)=1+
)•(x+2y)=1+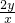 +
+ +2,结合条件,应用基本不等式即可.
+2,结合条件,应用基本不等式即可.解答:∵x,y∈(0,+∞),x+2y=1,
∴
 =(
=( )•(x+2y)=1+
)•(x+2y)=1+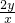 +
+ +2≥3+2
+2≥3+2 (当且仅当
(当且仅当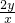 =
= ,即x=
,即x= -1时取“=”).
-1时取“=”).故答案为:3+2
 .
.点评:本题考查基本不等式,着重考查代入法及基本不等式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
给出下列四个式子(已知a>0且a≠1,x>y>0)①logax•logay=loga(x+y);②logax+logay=loga(xy);③loga
=loga(x-y);④logax-logay=
.其中正确的个数是( )
| x |
| y |
| logax |
| logay |
| A、0个 | B、1个 | C、2个 | D、3个 |
设方程f(x,y)=0表示定直线,M(x0,y0)是直线L外的定点,则方程f(x,y)-f(x0,y0)=0表示直线( C )
| A、过M与l相交,但与l不垂直 | B、过M且与l垂直 | C、过M与l平行 | D、以上都不对 |