题目内容
如图,四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
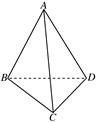
(1)求证:BC⊥AD;
(2)试问该四面体的体积是否存在最大值?若存在,求出这个最大值及此时棱长AD的大小;若不存在,请说明理由.

(1)求证:BC⊥AD;
(2)试问该四面体的体积是否存在最大值?若存在,求出这个最大值及此时棱长AD的大小;若不存在,请说明理由.
(1)见解析(2)最大值为8,此时棱长AD=2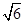 .
.
 .
.(1)证明:取BC的中点E,连结AE,DE,
∵△ABC与△DBC都是边长为4的正三角形,
∴AE⊥BC,DE⊥BC.
∵AE∩DE=E,
∴BC⊥平面AED,AD?平面AED,∴BC⊥AD.
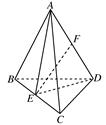
(2)由已知得,△AED为等腰三角形,且AE=ED=2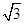 ,
,
设AD=x,F为棱AD的中点,
则EF=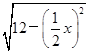 ,S△AED=
,S△AED=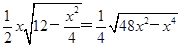 ,
,
V=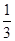 S△AED·(BE+CE)=
S△AED·(BE+CE)=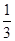
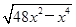 (0<x<4
(0<x<4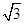 ),
),
当x2=24,即x=2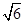 时,Vmax=8,
时,Vmax=8,
∴该四面体存在最大值,最大值为8,此时棱长AD=2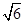 .
.
∵△ABC与△DBC都是边长为4的正三角形,
∴AE⊥BC,DE⊥BC.
∵AE∩DE=E,
∴BC⊥平面AED,AD?平面AED,∴BC⊥AD.

(2)由已知得,△AED为等腰三角形,且AE=ED=2
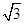 ,
,设AD=x,F为棱AD的中点,
则EF=
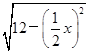 ,S△AED=
,S△AED=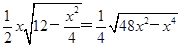 ,
,V=
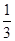 S△AED·(BE+CE)=
S△AED·(BE+CE)=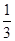
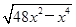 (0<x<4
(0<x<4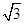 ),
),当x2=24,即x=2
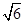 时,Vmax=8,
时,Vmax=8,∴该四面体存在最大值,最大值为8,此时棱长AD=2
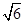 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,  为底面圆周上一点.
为底面圆周上一点.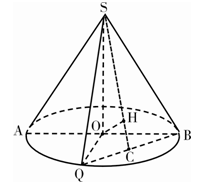
 的中点为
的中点为 ,
,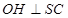 ,求证
,求证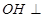 平面
平面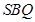 ;
;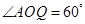 ,
,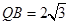 ,求此圆锥的全面积.
,求此圆锥的全面积.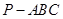 中,
中,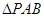 和
和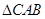 都是以
都是以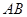 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,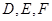 分别是
分别是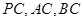 的中点.
的中点.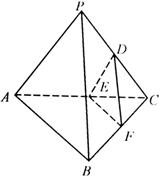
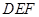 //平面
//平面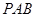 ;
;
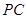 ;
;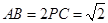 ,求三棱锥
,求三棱锥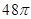 ,则此正方体边长为
,则此正方体边长为  ABCD的体积为
ABCD的体积为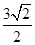 ,底面边长为
,底面边长为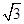 ,则以O为球心,OA为半径的球的表面积为 .
,则以O为球心,OA为半径的球的表面积为 . A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A
A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A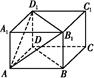
 ,则球的体积为 .
,则球的体积为 . 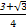 a2
a2 a2
a2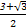 a2
a2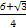 a2
a2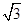 ,则棱锥O-ABCD的体积为________.
,则棱锥O-ABCD的体积为________.