题目内容
已知一元二次不等式f(x)<0的解集为{x|x<
或x>
},则f(10x)>0的解集为( )
| 1 |
| 10 |
| 1 |
| 2 |
| A、{x|x<-1或x>-lg 2} |
| B、{x|-1<x<-lg 2} |
| C、{x|x>-lg 2} |
| D、{x|x<-lg 2} |
考点:其他不等式的解法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:一元二次不等式f(x)<0的解集为{x|x<
或x>
},可得
,
是一元二次方程f(x)=0的两个实数根.于是f(10x)>0化为
<10x<
,解得即可.
| 1 |
| 10 |
| 1 |
| 2 |
| 1 |
| 10 |
| 1 |
| 2 |
| 1 |
| 10 |
| 1 |
| 2 |
解答:
解:∵一元二次不等式f(x)<0的解集为{x|x<
或x>
},
∴
,
是一元二次方程f(x)=0的两个实数根.
∴f(10x)>0化为
<10x<
,解得-1<x<-lg2.
∴f(10x)>0的解集为{x|-1<x<-lg2}.
故选B.
| 1 |
| 10 |
| 1 |
| 2 |
∴
| 1 |
| 10 |
| 1 |
| 2 |
∴f(10x)>0化为
| 1 |
| 10 |
| 1 |
| 2 |
∴f(10x)>0的解集为{x|-1<x<-lg2}.
故选B.
点评:本题考查了一元二次不等式的解集与相应的一元二次方程的实数根之间的关系、对数的运算性质,属于中档题.

练习册系列答案
相关题目
等比数列{an}中,首项a1=2,公比为3,Sn为其前n项和,则S4+a3等于( )
| A、44 | B、64 | C、98 | D、134 |
观察下列各数:1,2,2,4,8,32…,则该数列的第8项可能等于( )
| A、256 | B、1024 |
| C、4128 | D、8192 |
函数y=
的大致图象只能是( )
| 1 |
| x+2 |
A、 |
B、 |
C、 |
D、 |
已知集合A={(x,y)|
},B={(x,y)|x-y-1≤0},则集合A与B的关系为( )
|
| A、A∩B=∅ | B、A⊆B |
| C、B⊆A | D、A与B关系不确定 |
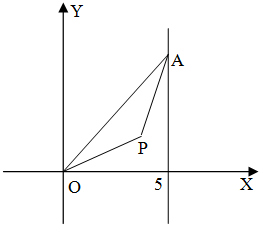 如图,点A在直线x=5上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按逆时针方向排列),求点P的轨迹方程.
如图,点A在直线x=5上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按逆时针方向排列),求点P的轨迹方程.