题目内容
设![]() 是椭圆
是椭圆![]() 上的两点,点
上的两点,点![]() 是线段
是线段![]() 的中点,线段
的中点,线段![]() 的垂直平分线与椭圆相交于
的垂直平分线与椭圆相交于![]() 两点.
两点.
(1) 确定实数![]() 的取值范围,并求直线
的取值范围,并求直线![]() 的方程;
的方程;
(2) 试判断是否存在这样的![]() ,使得
,使得![]() 四点在同一个圆上?并说明理由.
四点在同一个圆上?并说明理由.
(1)解法一:设直线![]() 的方程为
的方程为![]() ,代入
,代入![]()
整理得![]() ①
①
设![]() ,
,![]() ,② 且
,② 且![]()
由![]() 是线段
是线段![]() 的中点,得
的中点,得![]() ,解得
,解得![]() ,代入②得
,代入②得![]()
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() (5分)
(5分)
解法二:设![]() ,(点差)则有
,(点差)则有![]() ,因为
,因为![]() 是线段
是线段![]() 的中点,
的中点,![]()
又![]() 在椭圆内部,
在椭圆内部,![]() ,即
,即![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,即
,即![]()
(2)解法一:因为![]() 垂直平分
垂直平分![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,即
,即![]() ,代入椭圆方程,整理得
,代入椭圆方程,整理得![]()
设![]() ,
,![]() 的中点
的中点![]() ,
,![]() 且
且![]() ,即
,即![]() ,由弦长公式得
,由弦长公式得![]() ③,将直线
③,将直线![]() 的方程
的方程![]() 代入椭圆方程得
代入椭圆方程得![]() ④,同理可得
④,同理可得![]() ⑤ (9分)
⑤ (9分)
因为当![]() 时,
时,![]()
![]() ,所以
,所以![]()
假设存在![]() ,使
,使![]() 四点共圆,则
四点共圆,则![]() 必为圆的直径,点
必为圆的直径,点![]() 为圆心。点
为圆心。点![]() 到直线
到直线![]() 的距离
的距离![]() ⑥,
⑥,
于是![]() ,
,
故当![]() 时,
时,![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上 (12分)
为半径的圆上 (12分)

练习册系列答案
相关题目
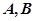 是椭圆
是椭圆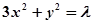 上的两点,点
上的两点,点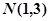 是线段
是线段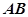 的中点,
的中点,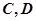 两点.
两点. 的取值范围,并求直线
的取值范围,并求直线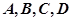 四点在同一个圆上?并说明理由.
四点在同一个圆上?并说明理由.