题目内容
已知数列 满足
满足 ,
, (
( 且
且 ).
).
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(Ⅱ)令 ,记数列
,记数列 的前
的前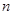 项和为
项和为 ,若
,若 恒为一个与
恒为一个与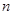 无关的常数
无关的常数 ,试求常数
,试求常数 和
和 .
.
(Ⅰ)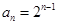 ;(Ⅱ)
;(Ⅱ)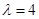 ,
, .
.
解析试题分析:(Ⅰ)求数列 的通项公式
的通项公式 ,这是已知
,这是已知 型求
型求 ,可仿
,可仿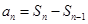 来求
来求 ,由
,由 ,可⇒
,可⇒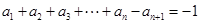 ,二式作差可得
,二式作差可得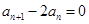 ,即
,即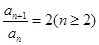 ,再求得
,再求得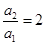 即可判断数列
即可判断数列 是首项为1,公比为2的等比数列,从而可求数列
是首项为1,公比为2的等比数列,从而可求数列 的通项公式
的通项公式 ;(Ⅱ)由(Ⅰ)得
;(Ⅱ)由(Ⅰ)得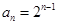 ,
,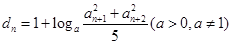 ,求得
,求得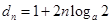 ,由等差数列的概念可判断
,由等差数列的概念可判断 是以
是以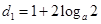 为首项,以
为首项,以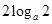 为公差的等差数列,由
为公差的等差数列,由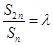 对任意正整数
对任意正整数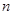 恒成立,即恒为一个与n无关的常数λ可得到关于λ的方程组,解之即可.
恒成立,即恒为一个与n无关的常数λ可得到关于λ的方程组,解之即可.
试题解析:(Ⅰ) 由题
由题 ①
①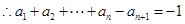 ②
②
由①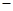 ②得:
②得: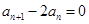 ,即
,即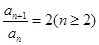 3分
3分
当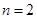 时,
时, ,
,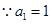 ,
,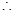
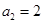 ,
,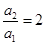
所以,数列 是首项为
是首项为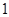 ,公比为
,公比为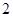 的等比数列
的等比数列
故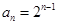 (
( ) 6分
) 6分
(Ⅱ)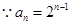 ,
,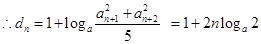
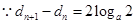 ,
,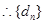 是以
是以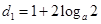 为首项,以
为首项,以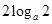 为公差的等差数列, 8分
为公差的等差数列, 8分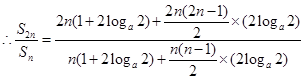
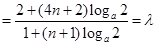
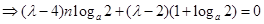 10分
10分
 恒为一个与
恒为一个与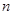 无关的常数
无关的常数 ,
,
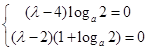
解之得: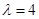 ,
, . 12分
. 12分
考点:等差数列的通项公式,等比数列的通项公式,数列的求和.

练习册系列答案
相关题目
 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数. 表示
表示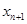 ;
; ,若
,若 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前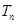 ,求
,求 的首项
的首项 ,公差
,公差 .且
.且 分别是等比数列
分别是等比数列 的
的 .
.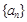 与
与 的通项公式;
的通项公式; 对任意自然数
对任意自然数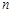 均有
均有
 成立,求
成立,求
 的值.
的值. 的前
的前 项和是
项和是 ,且
,且 .
. ,求适合方程
,求适合方程 的正整数
的正整数 中,
中, ,
, .
. 是等比数列,并求数列
是等比数列,并求数列 ,求数列
,求数列 的前
的前 项和
项和 .
. ,将函数
,将函数 在区间
在区间 内的全部极值点按从小到大的顺序排成数列
内的全部极值点按从小到大的顺序排成数列
 .
. ,数列
,数列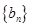 的前
的前 项和为
项和为 ,求
,求 的前
的前 项和为
项和为 ,
, .
. ,证明:数列
,证明:数列 是等比数列;
是等比数列; 的前
的前 .
.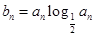 ,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值.
,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值.