题目内容
数列 的前
的前 项和为
项和为 ,
, .
.
(Ⅰ)设 ,证明:数列
,证明:数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
(Ⅰ)详见解析;(Ⅱ)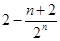 .
.
解析试题分析:(Ⅰ)利用递推关系式进行转化,然后通过构造数列证明数列 是等比数列;(Ⅱ)利用错位相减法求解数列
是等比数列;(Ⅱ)利用错位相减法求解数列 的前
的前 项和
项和 .
.
试题解析:(Ⅰ)因为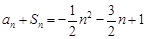 ,
,
所以 ① 当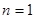 时,
时,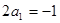 ,则
,则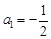 , 1分
, 1分
② 当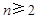 时,
时,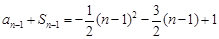 , 2分
, 2分
所以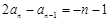 ,即
,即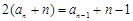 , 4分
, 4分
所以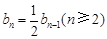 ,而
,而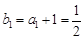 , 5分
, 5分
所以数列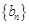 是首项为
是首项为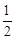 ,公比为
,公比为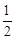 的等比数列,所以
的等比数列,所以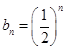 . 6分
. 6分
(Ⅱ)由(Ⅰ)得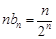 .
.
所以 ①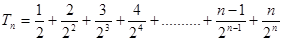 ,
,
②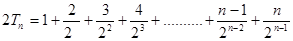 , 8分
, 8分
②-①得: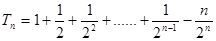 , 10分
, 10分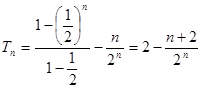 . 12分
. 12分
考点:1.数列的递推式;2.等比数列的证明;3.数列求和.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
 满足
满足 ,且
,且 ,其中
,其中 .
. 满足
满足 是否存在正整数m、n(1<m<n),使得
是否存在正整数m、n(1<m<n),使得 成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由。
成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由。 满足
满足 ,
, (
( 且
且 ).
). ;
; ,记数列
,记数列 的前
的前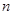 项和为
项和为 ,若
,若 恒为一个与
恒为一个与 ,试求常数
,试求常数 和
和

 的通项公式;
的通项公式; 求数列
求数列 的前
的前 项和
项和 。
。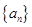 中,已知
中,已知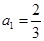 ,
,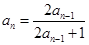 .
.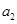 、
、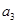 并判断
并判断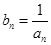 ,求证:
,求证: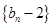 为等比数列;
为等比数列;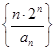 的前n项和
的前n项和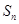 .
. 的各项均为正数,
的各项均为正数, ,
, .
. .证明:
.证明: 为等差数列,并求
为等差数列,并求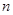 项和
项和 .
. }的前n项和为
}的前n项和为 ,
, ,
, .
. ,证明:数列
,证明:数列 是等比数列;
是等比数列; 的前
的前 项和
项和 ;
; ,
, .求不超过
.求不超过 的最大整数的值。
的最大整数的值。 中,
中, ,
, (
( 是常数,
是常数, ),且
),且 成公比不为
成公比不为 的等比数列.
的等比数列.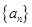 中,
中,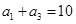 ,
,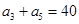 .设
.设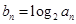 .
. 的通项公式;
的通项公式;  ,
,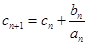 ,求证:
,求证: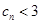 ;
;