题目内容
命题
①?x∈R,使sinx+cosx=2
②对?x∈R,sinx+
≥2
③对?x∈(0,
),tanx+
≥2
④?x∈R,使sinx+cosx=
,
其中真命题为( )
①?x∈R,使sinx+cosx=2
②对?x∈R,sinx+
| 1 |
| sinx |
③对?x∈(0,
| π |
| 2 |
| 1 |
| tanx |
④?x∈R,使sinx+cosx=
| 2 |
其中真命题为( )
分析:利用辅助角公式,将sinx+cosx化成正弦型函数的形式,求出其值域后,可以判断①,④的真假;
使用基本不等式求出sinx+
的值域,可以判断②的真假;由x∈(0,
),tanx>0,
>0,使用基本不等式可以判断③的真假;进而得到答案.
使用基本不等式求出sinx+
| 1 |
| sinx |
| π |
| 2 |
| 1 |
| tanx |
解答:解:∵sinx+cosx=
sin(x+
)∈[-
,
];故①?x∈R,使sinx+cosx=2,错误;
④?x∈R,使sinx+cosx=
,正确;
∵对?x∈R,sinx+
≤-2或sinx+
≥2,故②对?x∈R,sinx+
≥2,错误;
③对x∈(0,
),tanx>0,
>0,由基本不等式可得③?x∈(0,
),tanx+
≥2,正确;
故答案为:B
| 2 |
| π |
| 4 |
| 2 |
| 2 |
④?x∈R,使sinx+cosx=
| 2 |
∵对?x∈R,sinx+
| 1 |
| sinx |
| 1 |
| sinx |
| 1 |
| sinx |
③对x∈(0,
| π |
| 2 |
| 1 |
| tanx |
| π |
| 2 |
| 1 |
| tanx |
故答案为:B
点评:本题考查的知识点是全称命题和特称命题,其中根据基本不等式和正弦型函数的性质,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
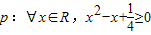 ②q:所有的正方形都是矩形③r:?x∈R,x2+2x+2≤0④s:至少有一个实数x,使x2-1=0( )
②q:所有的正方形都是矩形③r:?x∈R,x2+2x+2≤0④s:至少有一个实数x,使x2-1=0( )