题目内容
如果f(a+b)=f(a)•f(b)且f(1)=2,则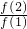 +
+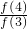 +
+ +…+
+…+ 等于
等于
- A.2003
- B.1001
- C.2004
- D.2002
C
分析:根据f(a+b)=f(a)•f(b)及 要求得结论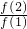 +
+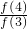 +
+ +…+
+…+ ,对a,b分别赋值为n,1转化为数列求和问题来解决.
,对a,b分别赋值为n,1转化为数列求和问题来解决.
解答:因为f(a+b)=f(a)•f(b),且f(1)=2,
所以令n,b=1,则f(n+1)=f(n)•f(1),即
∴数列{f(n)}是公比为2等比数列,
所以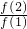 +
+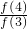 +
+ +…+
+…+ =2x1002=2004
=2x1002=2004
故得结论为2004.
故选C
点评:对于抽象函数的解决方法,通常采取赋值法,把抽象的数学问题转化为我们熟悉的数学问题加以解决,命题的立意新,是好题,属中档题.
分析:根据f(a+b)=f(a)•f(b)及 要求得结论
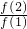 +
+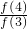 +
+ +…+
+…+ ,对a,b分别赋值为n,1转化为数列求和问题来解决.
,对a,b分别赋值为n,1转化为数列求和问题来解决.解答:因为f(a+b)=f(a)•f(b),且f(1)=2,
所以令n,b=1,则f(n+1)=f(n)•f(1),即

∴数列{f(n)}是公比为2等比数列,
所以
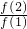 +
+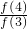 +
+ +…+
+…+ =2x1002=2004
=2x1002=2004故得结论为2004.
故选C
点评:对于抽象函数的解决方法,通常采取赋值法,把抽象的数学问题转化为我们熟悉的数学问题加以解决,命题的立意新,是好题,属中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
如果f(a+b)=f(a)•f(b)且f(1)=2,则
+
+
+…+
等于( )
| f(2) |
| f(1) |
| f(4) |
| f(3) |
| f(6) |
| f(5) |
| f(2004) |
| f(2003) |
| A、2003 | B、1001 |
| C、2004 | D、2002 |