题目内容
8.已知函数f(x)=|2x+1|+|2x-3|(1)求不等式f(x)≤6的解集;
(2)若关于x的不等式f(x)≤|a-2|的解集非空,求实数a的取值范围.
分析 (1)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(2)利用绝对值三角不等式求得f(x)的最小值为4,再根据|a-2|≥4,求得a的范围.
解答 解:(1)∵函数f(x)=|2x+1|+|2x-3|,∴不等式f(x)≤6 等价于$\left\{\begin{array}{l}{x<-\frac{1}{2}}\\{-2x-1+(3-2x)≤6}\end{array}\right.$①,或$\left\{\begin{array}{l}{-\frac{1}{2}≤x≤\frac{3}{2}}\\{2x+1+(3-2x)≤6}\end{array}\right.$②,或$\left\{\begin{array}{l}{x>\frac{3}{2}}\\{2x+1+2x-3≤6}\end{array}\right.$③.
解①求得-1≤x<-$\frac{1}{2}$;解②求得-$\frac{1}{2}$≤x≤$\frac{3}{2}$;解③求得 $\frac{3}{2}$<x≤2.
综合可得,原不等式的解集为[-1,2].
(2)∵f(x)=|2x+1|+|2x-3|≥|2x+1-(2x-3)|=4,则f(x)的最小值为4.
若关于x的不等式f(x)≤|a-2|的解集非空,则|a-2|≥4,a-2≥4,或 a-2≤-4,
求得a≥6,或a≤-2,
故a的范围为{a|a≥6,或a≤-2 }.
点评 本题主要考查绝对值不等式的解法,绝对值三角不等式,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
3.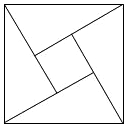 在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则sin2θ-cos2θ的值等于( )
在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则sin2θ-cos2θ的值等于( )
 在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则sin2θ-cos2θ的值等于( )
在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则sin2θ-cos2θ的值等于( )| A. | 1 | B. | -$\frac{7}{25}$ | C. | $\frac{7}{25}$ | D. | -$\frac{24}{25}$ |
20.在△ABC中,内角A、B、C所对的边为a、b、c,若c2≤a2+b2-ab,则C的取值范围为( )
| A. | (0,$\frac{π}{3}$] | B. | [$\frac{π}{6}$,π) | C. | [$\frac{π}{3}$,π) | D. | (0,$\frac{π}{6}$] |
17.已知集合M=$\{x|\frac{2-x}{x+1}≥0\}$,N={y|y=lnx},则M∩N=( )
| A. | (0,2] | B. | (-1,2] | C. | (-1,+∞) | D. | R |
18.已知甲、乙、丙三种食物的维生素及成本入戏表实数:
某学校食堂欲将这三种食物混合加工成100kg混合食物,且要求混合食物中至少需要含35000单位的维生素C及40000单位的维生素D.
(1)设所用食物甲、乙、丙的质量分别为xkg,ykg,100-x-ykg(x≥0,y≥0),试列出x,y满足的数学关系式,并画出相应的平面区域;
(2)用x,y表示这100kg混合食物的成本z,求出z的最小值.
| 食物类型 | 甲 | 乙 | 丙 |
| 维生素C(单位/kg) | 300 | 500 | 300 |
| 维生素D(单位/kg) | 700 | 100 | 300 |
| 成本(元/kg) | 5 | 4 | 3 |
(1)设所用食物甲、乙、丙的质量分别为xkg,ykg,100-x-ykg(x≥0,y≥0),试列出x,y满足的数学关系式,并画出相应的平面区域;
(2)用x,y表示这100kg混合食物的成本z,求出z的最小值.