题目内容
已知
(1)若 ,求
,求 的极大值点;
的极大值点;
(2)若 且
且 存在单调递减区间,求
存在单调递减区间,求 的取值范围.
的取值范围.

(1)若
 ,求
,求 的极大值点;
的极大值点;(2)若
 且
且 存在单调递减区间,求
存在单调递减区间,求 的取值范围.
的取值范围.(1)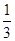 ;(2)
;(2)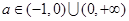 .
.
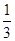 ;(2)
;(2)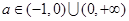 .
.试题分析:)(1)极值点的求法是利用导数知识求解,求出
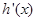 ,求得
,求得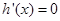 的解
的解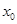 ,然后确定当
,然后确定当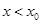 以及
以及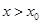 时的
时的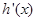 的符号,若当
的符号,若当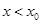 时,
时,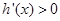 ,当
,当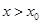 时,
时,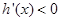 ,则
,则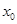 是极大值点,反之是极小值点;(2)
是极大值点,反之是极小值点;(2) 时,
时,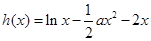 ,它存在单调递减区间,说明不等式
,它存在单调递减区间,说明不等式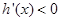 有解,考虑到
有解,考虑到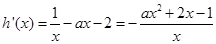 且
且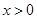 ,因此不等式
,因此不等式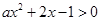 在
在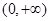 上有解,下面利用二次函数知识就可得出结论,当
上有解,下面利用二次函数知识就可得出结论,当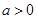 时,
时,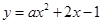 的图象是开口向上的抛物线,在
的图象是开口向上的抛物线,在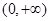 上一定有解,当
上一定有解,当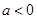 时,
时,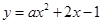 的图象是开口向下的抛物线,在
的图象是开口向下的抛物线,在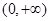 上要有解,则
上要有解,则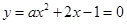 至少有一正根,由于此时对称轴为
至少有一正根,由于此时对称轴为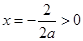 ,故只要
,故只要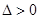 ,方程一定有正根.
,方程一定有正根.试题解析:
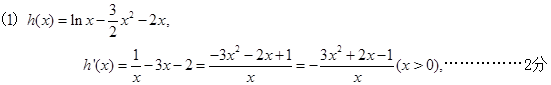 令h′(x)=0,则3x2+2x-1=0,x1=-1,x2=
令h′(x)=0,则3x2+2x-1=0,x1=-1,x2=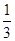 . 3分
. 3分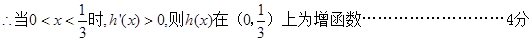
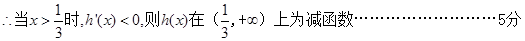
所以
 的极大值点为
的极大值点为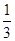 . 6分
. 6分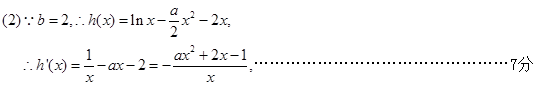
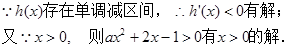
① 当a>0,
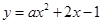 为开口向上的抛物线,
为开口向上的抛物线,而
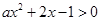 总有
总有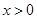 的解; 8分
的解; 8分② 当a<0,
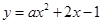 为开口向下的抛物线,
为开口向下的抛物线,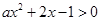 有
有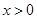 的解;
的解;则
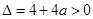 且方程
且方程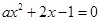 至少有一正根,此时-1<a<0 11分
至少有一正根,此时-1<a<0 11分综上所述,
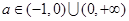 . 12分
. 12分
练习册系列答案
相关题目
 .
. 上总存在相异的两点
上总存在相异的两点 ,使得曲线
,使得曲线 .
.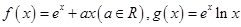 (e为自然对数的底数).
(e为自然对数的底数).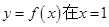 处的切线为
处的切线为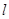 ,若
,若 ,求a的值;
,求a的值;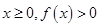 恒成立,试确定
恒成立,试确定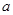 的取值范围;
的取值范围; 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由. 是自然对数的底数,函数
是自然对数的底数,函数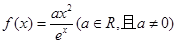 .
. 的单调递增区间;
的单调递增区间;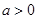 时,函数
时,函数 ,求
,求 的值.
的值.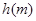 与起跳后的时间
与起跳后的时间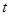
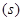 存在函数关系
存在函数关系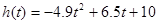 ,则瞬时速度为0
,则瞬时速度为0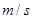 的时刻是( )
的时刻是( )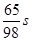
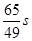
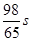
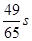
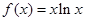 ,若
,若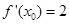 ,则
,则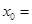 ( )
( )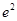
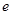
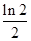
 在点(1,1)处的切线与
在点(1,1)处的切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,则
,则 的值为
的值为


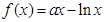 ,
,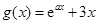 ,其中
,其中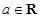 .
. 的极值;
的极值;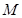 ,使
,使 在区间
在区间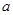 的取值范围.
的取值范围.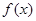 的导数为
的导数为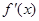 ,且
,且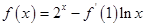 ,则
,则 的值是 .
的值是 .