题目内容
2.设向量$\overrightarrow{a}$,$\overrightarrow{b}$满足:|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$|=2,$\overrightarrow{b}$•($\overrightarrow{b}$+$\overrightarrow{a}$)=0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角大小为$\frac{2π}{3}$.分析 将等式展开,利用数量积公式得到关于向量夹角的等式求之.
解答 解:由已知,|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$|=2,$\overrightarrow{b}$•($\overrightarrow{b}$+$\overrightarrow{a}$)=0,设夹角为α,所以${\overrightarrow{b}}^{2}+\overrightarrow{b}•\overrightarrow{a}=0$,所以1+2cosα=0,解答cosα=$-\frac{1}{2}$,
所以α=$\frac{2π}{3}$;
故答案为;$\frac{2π}{3}$.
点评 本题考查了向量的数量积于是以及利用数量积公式求夹角;属于基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
12. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{6}$ | C. | 3 | D. | 2$\sqrt{3}$ |
13.直线y=ax+b通过第一、二、三象限,则圆(x+a)2+(y+b)2=r2(r>0)的圆心位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.若函数f(x)=a+|x|+log2(x2+2)有且只有一个零点,则实数a的值是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
17.已知集合A=|x|x>1|,B=|xy=$\sqrt{9-{x}^{2}}$|.那么A∩B=( )
| A. | [-3,3] | B. | (-1,3] | C. | (1,3] | D. | (1,3) |
7.已知6枝玫瑰与3枝康乃馨的价格之和大于24元,而4枝玫瑰与4枝康乃馨的价格之和小于20元,那么2枝玫瑰和3枝康乃馨的价格的比较结果是( )
| A. | 2枝玫瑰的价格高 | B. | 3枝康乃馨的价格高 | ||
| C. | 价格相同 | D. | 不确定 |
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数,
为参数,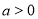 ),在以坐标原点为极点,
),在以坐标原点为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 .
. 的极坐标方程为
的极坐标方程为 ,其中
,其中 满足
满足 ,若曲线
,若曲线 的公共点都在
的公共点都在 上,求
上,求 .
.