题目内容
已知函数f(x)=sin2x+cos2x.
(1)求f(x)的最小正周期、最大值、最小值;
(2)试说明f(x)是怎样由f(x)=sinx变换得来的.
(1)求f(x)的最小正周期、最大值、最小值;
(2)试说明f(x)是怎样由f(x)=sinx变换得来的.
考点:函数y=Asin(ωx+φ)的图象变换,两角和与差的正弦函数,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)提取
后由两角和的正弦化简,则f(x)的最小正周期、最大值、最小值可求;
(2)直接利用三角函数图象先改变周期后平移的办法得答案.
| 2 |
(2)直接利用三角函数图象先改变周期后平移的办法得答案.
解答:
解:(1)f(x)=sin2x+cos2x=
(
sin2x+
cos2x)=
sin(2x+
).
∴f(x)的最小正周期、最大值、最小值分别为π、
、-
;
(2)把f(x)=sinx的图象上所有点的横坐标缩小到原来的
,纵坐标不变得到y=sin2x,
再把y=sin2x向左平移
个单位得到y=sin(2x+
),最后把y=sin(2x+
)图象上点的横坐标不变,纵坐标扩大到原来的
倍得到.
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
∴f(x)的最小正周期、最大值、最小值分别为π、
| 2 |
| 2 |
(2)把f(x)=sinx的图象上所有点的横坐标缩小到原来的
| 1 |
| 2 |
再把y=sin2x向左平移
| π |
| 8 |
| π |
| 4 |
| π |
| 4 |
| 2 |
点评:本题考查了y=Asin(ωx+φ)型函数的图象平移,关键是注意平移的单位,是基础题.

练习册系列答案
相关题目
 如图,已知平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,∠CBF=90°,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2,G为CE中点.
如图,已知平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,∠CBF=90°,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2,G为CE中点.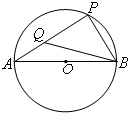 如图,AB是半径为3的圆O的直径,P是圆O上异于A,B的一点Q是线段AP上靠近A的三等分点,且
如图,AB是半径为3的圆O的直径,P是圆O上异于A,B的一点Q是线段AP上靠近A的三等分点,且