题目内容
(本小题满分14分)
在正三棱柱 中,点
中,点 是
是 的中点,
的中点, .
.
(1)求证: ∥平面
∥平面 ;
;
(2)试在棱 上找一点
上找一点 ,使
,使 .
.
(1)详见解析(2) 为
为 的中点.
的中点.
【解析】
试题分析:(1)证明线面平行,一般利用线面平行判定定理进行证明,即先从线线平行出发,这可利用三角形中位线性质进行证明:连接 ,交
,交 于点
于点 ,则
,则 、
、 分别是
分别是 、
、 的中点,所以
的中点,所以 ∥
∥ .从而可证
.从而可证 ∥平面
∥平面 .(2)找一点目的是证线线垂直,故从垂直角度找:利用正方形性质,边的中点与对边顶点连线存在垂直关系,故取
.(2)找一点目的是证线线垂直,故从垂直角度找:利用正方形性质,边的中点与对边顶点连线存在垂直关系,故取 为
为 的中点.再根据线面垂直判定及性质定理进行论证.
的中点.再根据线面垂直判定及性质定理进行论证.
试题解析:(1)证明:连接 ,交
,交 于点
于点 , 连接
, 连接 .
.

∵ 、
、 分别是
分别是 、
、 的中点,
的中点,
∴ ∥
∥ . 3分
. 3分
∵ 平面
平面 ,
, 平面
平面 ,
,
∴ ∥平面
∥平面 . 6分
. 6分
(2) 为
为 的中点. 7分
的中点. 7分
证明如下:
∵在正三棱柱 中,
中, ,∴四边形
,∴四边形 是正方形.
是正方形.
∵ 为
为 的中点,
的中点, 是
是 的中点,∴
的中点,∴ , 9分
, 9分
∴ ,
, .
.
又∵ ,
,
 ,∴
,∴ . 11分
. 11分
∵ 是正三角形,
是正三角形, 是
是 的中点,
的中点,
∴ .
.
∵平面 平面
平面 , 平面
, 平面 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 .
.
∵ 平面
平面 ,
,
∴
 . 13分
. 13分
∵ ,
,
∴ 平面
平面 .
.
∵ 平面
平面 ,
,
∴ . 14分
. 14分
考点:线面平行判定定理,线面垂直判定及性质定理

练习册系列答案
相关题目
 ,
, ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( ) (B)
(B) (C)
(C) (D)
(D)
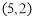 ,且在
,且在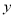 轴上的截距是在
轴上的截距是在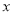 轴上的截距的
轴上的截距的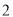 倍的直线方程是( )
倍的直线方程是( ) 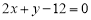 B.
B.
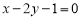 D.
D.
 ,则
,则 .
. 分别是椭圆
分别是椭圆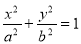
 的上顶点和右焦点,直线
的上顶点和右焦点,直线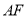 与椭圆交于另一点
与椭圆交于另一点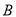 ,过中心
,过中心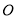 作直线
作直线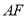 的平行线交椭圆于
的平行线交椭圆于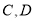 两点,若
两点,若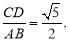 则椭圆的离心率为 .
则椭圆的离心率为 .
 中,各项都是正数,且
中,各项都是正数,且 成等差数列,则
成等差数列,则 等于 .
等于 . 的离心率等于( )
的离心率等于( ) B.
B. C.
C. 

 ,其中
,其中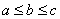 的,对于下列结论:①
的,对于下列结论:①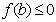 ; ②若
; ②若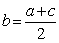 ,则
,则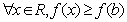 ;
;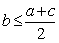 ,则
,则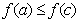 ;④
;④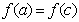 成立充要条件为
成立充要条件为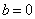 .
.