题目内容
已知实数x，y满足约束条件
，则x2+y2-10x-8y+41的最小值是 ．
|
考点：简单线性规划的应用
专题：计算题,作图题,不等式的解法及应用
分析：由题意作出其平面区域，x2+y2-10x-8y+41=（x-5）2+（y-4）2是阴影内的点到点（5，4）的距离的平方，由几何意义可得．
解答：
解：由题意作出其平面区域，
x2+y2-10x-8y+41=（x-5）2+（y-4）2，是阴影内的点到点（5，4）的距离的平方；
故当点为（1，1）时，有最小值，
故最小值为1+1-10-8+41=25，
故答案为：25．
x2+y2-10x-8y+41=（x-5）2+（y-4）2，是阴影内的点到点（5，4）的距离的平方；
故当点为（1，1）时，有最小值，
故最小值为1+1-10-8+41=25，
故答案为：25．
点评：本题考查了简单线性规划，作图要细致认真，属于中档题．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
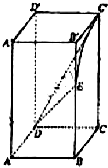如图，四棱柱ABCD-A′B′C′D′中，底面ABCD为正方形，侧棱AA′⊥底面ABCD，AB=3| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
台风中心从A地以20km/h的速度向东偏北45°方向移动，离台风中心30km内的地区为危险区，城市B在A的正东40km处，B城市处于危险区内的时间为（ ）
| A、0.5h | B、1h |
| C、1.5h | D、2h |