题目内容
已知向量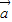
=（2，3），
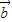=（cosθ，sinθ）且
∥
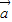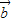，则tanθ=（ ）A．
B．-
C．
D．-
【答案】分析：根据两个向量共线的性质，得到2sinθ-3cosθ=0，再同角三角函数的基本关系求得 tanθ的值．
解答：解：∵向量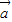
=（2，3），
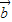=（cosθ，sinθ），且
∥
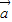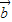，∴2sinθ-3cosθ=0，
∴tanθ=
，故选A．
点评：本题考查同角三角函数的基本关系，两个向量共线的性质，得到2sinθ-3cosθ=0，是解题的关键．
解答：解：∵向量
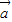=（2，3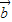），=（cosθ，sinθ），且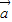∥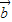，∴2sinθ-3cosθ=0，∴tanθ=
，故选A．点评：本题考查同角三角函数的基本关系，两个向量共线的性质，得到2sinθ-3cosθ=0，是解题的关键．
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
已知向量
=（-2，3），
=（x，6），则“x=9”是“
∥
”的（ ）
| a |
| b |
| a |
| b |
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |