题目内容
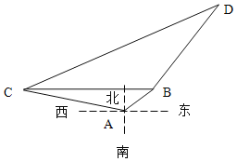
【题目】钓鱼岛及其附属岛屿是中国固有领土，如图：点A、B、C分别表示钓鱼岛、南小岛、黄尾屿，点C在点A的北偏东47°方向，点B在点C的南偏西36°方向，点B在点A的南偏东79°方向，且A、B两点的距离约为3海里.
（1）求A、C两点间的距离；（精确到0.01）
（2）某一时刻，我国一渔船在A点处因故障抛锚发出求救信号.一艘R国舰艇正从点C正东10海里的点P处以18海里/小时的速度接近渔船，其航线为P
CA（直线行进），而我东海某渔政船正位于点A南偏西60°方向20海里的点Q处，收到信号后赶往救助，其航线为先向正北航行8海里至点M处，再折向点A直线航行，航速为22海里/小时.渔政船能否先于R国舰艇赶到进行救助？说明理由．
【答案】(1)14.25海里；（2）渔政船能先于R国舰艇赶到进行救助．
【解析】
试题（1）这是解三角形问题，图形中
，已知
，要求
，因此由正弦定理知应该知道它们所对的两角，由题中已知的三个方位角，可求出
，
，
，故易求得结论；（2）只要求出两船到达
点的时间即可，
国舰艇路程为
，我渔政船路程为
，这里要在
中求出
，已知
，因此应用余弦定理可求出，从而得出结论．
试题解析：（1）求得
，
由
海里.
（2）R国舰艇的到达时间为：
小时.
在
中，
得
海里，
所以渔政船的到达时间为：
小时.
因为
，所以渔政船先到.
答：渔政船能先于R国舰艇赶到进行救助.
【题目】从某校随机抽取200名学生,获得了他们一周课外阅读时间(单位:h)的数据,整理得到数据的频数分布表和频率分布直方图(如图).
编 号 | 分 组 | 频 数 |
1 | [0,2) | 12 |
2 | [2,4) | 16 |
3 | [4,6) | 34 |
4 | [6,8) | 44 |
续 表
编 号 | 分 组 | 频 数 |
5 | [8,10) | 50 |
6 | [10,12) | 24 |
7 | [12,14) | 12 |
8 | [14,16) | 4 |
9 | [16,18] | 4 |
合计 | 200 |
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12 h的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
