题目内容
求函数f(x)=(
)2x-x2的定义域、值域和单调区间.
| 1 |
| 2 |
考点:指数型复合函数的性质及应用
专题:函数的性质及应用
分析:函数f(x)=(
)2x-x2的定义域为R;令t=2x-x2,则y=f(x)=(
)t,结合指数函数的图象和性质及二次函数的图象和性质,可得函数f(x)=(
)2x-x2的值域和单调区间.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:函数f(x)=(
)2x-x2的定义域为R;
令t=2x-x2,则y=f(x)=(
)t,
∵t=2x-x2∈(-∞,1],
∴y=f(x)=(
)t∈[
,+∞),
即函数f(x)=(
)2x-x2的值域为[
,+∞),
∵t=2x-x2在(-∞,1]上为增函数,在[1,+∞)上为减函数,
y=(
)t为减函数,
∴函数f(x)=(
)2x-x2的单调递增区间为[1,+∞);单调递减区间为(-∞,1]
| 1 |
| 2 |
令t=2x-x2,则y=f(x)=(
| 1 |
| 2 |
∵t=2x-x2∈(-∞,1],
∴y=f(x)=(
| 1 |
| 2 |
| 1 |
| 2 |
即函数f(x)=(
| 1 |
| 2 |
| 1 |
| 2 |
∵t=2x-x2在(-∞,1]上为增函数,在[1,+∞)上为减函数,
y=(
| 1 |
| 2 |
∴函数f(x)=(
| 1 |
| 2 |
点评:本题考查的知识点是指数函数的图象和性质,二次函数的图象和性质,复合函数的值域及单调性,难度中档.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知点P(sinα-cosα,2)在第二象限,则α的一个变化区间是( )
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(
|
数列{an}的前n项和为Sn,若an=
,则S7=( )
| 1 |
| n(n+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
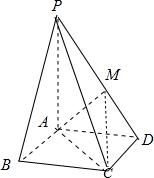 如图,四棱锥P-ABCD的底面ABCD是矩形,侧棱PA⊥底面ABCD,PA=2
如图,四棱锥P-ABCD的底面ABCD是矩形,侧棱PA⊥底面ABCD,PA=2