Question

假设通过点（0，1）和点（4，a）与x轴相切的圆只有一个，试求a的值和此圆的方程.

Answer 1

解析：设圆心为（α,β）,∵圆过点（0，1）且与x轴相切，则β＞0,且β为半径，于是圆的方程可写为（x-α）²+(y-β)²=β².

∵该圆过点（0，1）、（4，a）,

则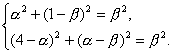消去β,得（1-a）α²-8α+(a²-a+16)=0.                 ①

(1)当a=1时，α=2,β=；

(2)当a≠1时，要使满足条件的圆只有一个，需Δ=0，即a³-2a+17a=0a=0,代入①得α²-8α+16=0,∴α=4,β=.

综上可知，当a=1时，满足条件的圆只有一个，其方程为（x-2）²+(y-)²=；当a=0时，满足条件的圆仅有一个，其方程为（x-4）²+(y-)²=.