题目内容
设f(x)=cosx+
-1.
(Ⅰ)求证:当x≥0时,f(x)≥0;
(Ⅱ)若不等式eax≥sinx-cosx+2对任意的x≥0恒成立,求实数a的取值范围.
| x2 |
| 2 |
(Ⅰ)求证:当x≥0时,f(x)≥0;
(Ⅱ)若不等式eax≥sinx-cosx+2对任意的x≥0恒成立,求实数a的取值范围.
考点:函数恒成立问题
专题:综合题,导数的综合应用
分析:(Ⅰ)求导数,证明f'(x)=x-sinx为增函数,从而可得f(x)在x≥0时为增函数,即可证明当x≥0时,f(x)≥0;
(Ⅱ)解法一:证明以
+x+1≥sinx-cosx+2,设G(x)=ex-
-x-1,证明G(x)为增函数,所以G(x)≥G(0)=0,所以ex≥sinx-cosx+2对任意的x≥0恒成立,再分类讨论,利用不等式eax≥sinx-cosx+2对任意的x≥0恒成立,即可求实数a的取值范围;
解法二:因为eax≥sinx-cosx+2等价于ax≥ln(sinx-cosx+2),设g(x)=ax-ln(sinx-cosx+2),分类讨论,即可求实数a的取值范围.
(Ⅱ)解法一:证明以
| x2 |
| 2 |
| x2 |
| 2 |
解法二:因为eax≥sinx-cosx+2等价于ax≥ln(sinx-cosx+2),设g(x)=ax-ln(sinx-cosx+2),分类讨论,即可求实数a的取值范围.
解答:
(Ⅰ)证明:f(x)=cosx+
-1(x≥0),则f'(x)=x-sinx,
设φ(x)=x-sinx,则φ'(x)=1-cosx,…(2分)
当x≥0时,φ'(x)=1-cosx≥0,即f'(x)=x-sinx为增函数,
所以f'(x)≥f'(0)=0,
即f(x)在x≥0时为增函数,所以f(x)≥f(0)=0. …(4分)
(Ⅱ)解法一:由(Ⅰ)知x≥0时,sinx≤x,cosx≥-
+1,
所以
+x+1≥sinx-cosx+2,…(6分)
设G(x)=ex-
-x-1,则G'(x)=ex-x-1,
设g(x)=ex-x-1,则g'(x)=ex-1,
当x≥0时g'(x)=ex-1≥0,所以g(x)=ex-x-1为增函数,
所以g(x)≥g(0)=0,所以G(x)为增函数,所以G(x)≥G(0)=0,
所以ex≥sinx-cosx+2对任意的x≥0恒成立.…(8分)
又x≥0,a≥1时,eax≥ex,
所以a≥1时eax≥sinx-cosx+2对任意的x≥0恒成立.…(9分)
当a<1时,设h(x)=eax-sinx+cosx-2,则h'(x)=aeax-cosx-sinx,h'(0)=a-1<0,
所以存在实数x0>0,使得任意x∈(0,x0),均有h'(x)<0,所以h(x)在(0,x0)为减函数,
所以在x∈(0,x0)时h(x)<h(0)=0,所以a<1时不符合题意.
综上,实数a的取值范围为[1,+∞).…(12分)
(Ⅱ)解法二:因为eax≥sinx-cosx+2等价于ax≥ln(sinx-cosx+2)…(6分)
设g(x)=ax-ln(sinx-cosx+2),则g′(x)=a-
可求
∈[-1,1],…(8分)
所以当a≥1时,g'(x)≥0恒成立,g(x)在[0,+∞)是增函数,
所以g(x)≥g(0)=0,即ax≥ln(sinx-cosx+2),即eax≥sinx-cosx+2
所以a≥1时,eax≥sinx-cosx+2对任意x≥0恒成立.…(9分)
当a<1时,一定存在x0>0,满足在(0,x0)时,g'(x)<0,
所以g(x)在(0,x0)是减函数,此时一定有g(x)<g(0)=0,
即ax<ln(sinx-cosx+2),即eax<sinx-cosx+2,不符合题意,故a<1不能满足题意,
综上所述,a≥1时,eax≥sinx-cosx+2对任意x≥0恒成立.…(12分)
| x2 |
| 2 |
设φ(x)=x-sinx,则φ'(x)=1-cosx,…(2分)
当x≥0时,φ'(x)=1-cosx≥0,即f'(x)=x-sinx为增函数,
所以f'(x)≥f'(0)=0,
即f(x)在x≥0时为增函数,所以f(x)≥f(0)=0. …(4分)
(Ⅱ)解法一:由(Ⅰ)知x≥0时,sinx≤x,cosx≥-
| x2 |
| 2 |
所以
| x2 |
| 2 |
设G(x)=ex-
| x2 |
| 2 |
设g(x)=ex-x-1,则g'(x)=ex-1,
当x≥0时g'(x)=ex-1≥0,所以g(x)=ex-x-1为增函数,
所以g(x)≥g(0)=0,所以G(x)为增函数,所以G(x)≥G(0)=0,
所以ex≥sinx-cosx+2对任意的x≥0恒成立.…(8分)
又x≥0,a≥1时,eax≥ex,
所以a≥1时eax≥sinx-cosx+2对任意的x≥0恒成立.…(9分)
当a<1时,设h(x)=eax-sinx+cosx-2,则h'(x)=aeax-cosx-sinx,h'(0)=a-1<0,
所以存在实数x0>0,使得任意x∈(0,x0),均有h'(x)<0,所以h(x)在(0,x0)为减函数,
所以在x∈(0,x0)时h(x)<h(0)=0,所以a<1时不符合题意.
综上,实数a的取值范围为[1,+∞).…(12分)
(Ⅱ)解法二:因为eax≥sinx-cosx+2等价于ax≥ln(sinx-cosx+2)…(6分)
设g(x)=ax-ln(sinx-cosx+2),则g′(x)=a-
| sinx+cosx |
| sinx-cosx+2 |
可求
| sinx+cosx |
| sinx-cosx+2 |
所以当a≥1时,g'(x)≥0恒成立,g(x)在[0,+∞)是增函数,
所以g(x)≥g(0)=0,即ax≥ln(sinx-cosx+2),即eax≥sinx-cosx+2
所以a≥1时,eax≥sinx-cosx+2对任意x≥0恒成立.…(9分)
当a<1时,一定存在x0>0,满足在(0,x0)时,g'(x)<0,
所以g(x)在(0,x0)是减函数,此时一定有g(x)<g(0)=0,
即ax<ln(sinx-cosx+2),即eax<sinx-cosx+2,不符合题意,故a<1不能满足题意,
综上所述,a≥1时,eax≥sinx-cosx+2对任意x≥0恒成立.…(12分)
点评:本题考查函数恒成立问题,考查导数知识的运用,考查分类讨论的数学思想,考查学生分析解决问题的能力,难度大.

练习册系列答案
相关题目
若函数f(x)满足:f(x)-4f(
)=x,则|f(x)|的最小值为( )
| 1 |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
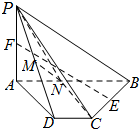 如图所示,四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,∠ABC=90°,AP=BC=2,AB=3,CD=1,E、F、M分别是BC、PA、PD的中点.
如图所示,四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,∠ABC=90°,AP=BC=2,AB=3,CD=1,E、F、M分别是BC、PA、PD的中点.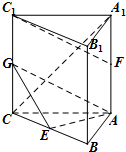 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB⊥AC,AC=AB=AA1,E、F分别是棱BC,A1A的中点,G为棱CC1上的一点,且C1F∥平面AEG.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB⊥AC,AC=AB=AA1,E、F分别是棱BC,A1A的中点,G为棱CC1上的一点,且C1F∥平面AEG.