题目内容
设函数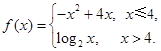 若函数
若函数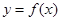 在区间
在区间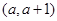 上单调递增,则实数
上单调递增,则实数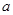 的取值范围是( )
的取值范围是( )
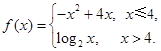 若函数
若函数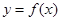 在区间
在区间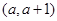 上单调递增,则实数
上单调递增,则实数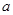 的取值范围是( )
的取值范围是( )A.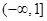 | B.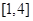 |
C.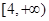 | D. |
D
试题分析:由函数
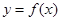 的图像可知,在
的图像可知,在 和
和 上是递增的,在
上是递增的,在 上是递减的,故函数
上是递减的,故函数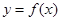 在区间
在区间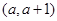 上单调递增,则
上单调递增,则 或
或 ,即
,即 或
或 ,故选D.
,故选D.
练习册系列答案
相关题目
题目内容
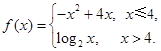 若函数
若函数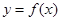 在区间
在区间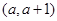 上单调递增,则实数
上单调递增,则实数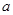 的取值范围是( )
的取值范围是( )A.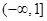 | B.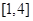 |
C.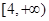 | D. |
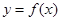 的图像可知,在
的图像可知,在 和
和 上是递增的,在
上是递增的,在 上是递减的,故函数
上是递减的,故函数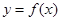 在区间
在区间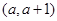 上单调递增,则
上单调递增,则 或
或 ,即
,即 或
或 ,故选D.
,故选D.