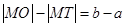题目内容
在抛物线y2=2px上,横坐标为4的点到焦点的距离为5,则p的值为( )
A. | B.1 | C.4 | D.2 |
D
解析试题分析:根据抛物线的定义,在抛物线y2=2px上,横坐标为4的点到焦点的距离为5,那么可知5=4+ ,p=2,故可知选D.
,p=2,故可知选D.
考点:本试题考查了抛物线的性质运用。
点评:解决该试题的关键是对于抛物线定义的运用,结合曲线上点到焦点的距离等于其到准线的距离,属于基础题。

练习册系列答案
相关题目
如图,用与底面成 角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
A. | B. | C. | D.非上述结论 |
椭圆 和双曲线
和双曲线 的公共焦点为
的公共焦点为 ,
, 是两曲线的一个交点,那么
是两曲线的一个交点,那么 的值是( )
的值是( )
A. | B. | C. | D. |
双曲线 的渐近线方程为
的渐近线方程为
A.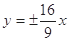 | B. | C. | D. |
已知 是椭圆
是椭圆 的两个焦点,
的两个焦点,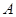 为椭圆上的一点,且
为椭圆上的一点,且 ,则
,则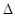
 的面积是( )
的面积是( )
| A.7 | B. | C. | D. |
抛物线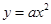 的焦点坐标是( )
的焦点坐标是( )
A. | B.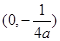 | C. | D. |
方程2x2+ky2=1表示的是焦点在y轴上的椭圆,则实数k的取值范围是( )
| A.(0,+∞) | B.(2,+∞) | C.(0,2) | D.(0,1) |
 (a>b>0)的两个焦点,过F2作椭圆的弦AB,若△AF1B的周长为16,椭圆的离心率
(a>b>0)的两个焦点,过F2作椭圆的弦AB,若△AF1B的周长为16,椭圆的离心率 ,则椭圆的方程为( )
,则椭圆的方程为( )



 的左焦点
的左焦点 引圆
引圆 的切线,切点为
的切线,切点为 ,延长
,延长 交双曲线右支于
交双曲线右支于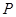 点,若
点,若 为线段
为线段 的中点,
的中点, 为坐标原点,则
为坐标原点,则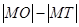 与
与 的大小关系为 ( )
的大小关系为 ( )