题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)设函数![]() ,试判断函数
,试判断函数![]() 是否存在最小值,若存在,求出最小值,若不存在,请说明理由.
是否存在最小值,若存在,求出最小值,若不存在,请说明理由.
(Ⅲ)当![]() 时,写出
时,写出![]() 与
与![]() 的大小关系.
的大小关系.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)
;(Ⅱ)见解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)先利用导数求出切线的斜率,然后再求得切点坐标,最后写出切线方程即可;
(Ⅱ)对a进行分类讨论,利用导数研究函数的最值,当![]() 时,函数
时,函数![]() 不存在最小值;当
不存在最小值;当![]() 时,函数
时,函数![]() 有最小值
有最小值![]() .
.
(Ⅲ)当![]() 时,
时,![]() 与
与![]() 的大小关系等价于
的大小关系等价于![]() 与
与![]() 的大小关系,
的大小关系,
令![]() ,通过研究
,通过研究![]() 的单调性和极值,进而可得
的单调性和极值,进而可得![]() ,从而可得结果.
,从而可得结果.
(Ⅰ)当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,因此
,因此![]() ,
,
又因为![]() ,所以切点为
,所以切点为![]() ,
,
所以切线方程为![]() ;
;
(Ⅱ)![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ;
;
(1)当![]() ,即
,即![]() 时,
时,
因为![]() ,所以
,所以![]() ,故
,故![]() ,
,
此时函数![]() 在
在![]() 上单调递增,
上单调递增,
所以函数![]() 不存在最小值;
不存在最小值;
(2)当![]() ,即
,即![]() 时,
时,
令![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
![]() 与
与![]() 在
在![]() 上的变化情况如下:
上的变化情况如下:
|
|
|
|
| 0 | + | |
| ↘ | 极小值 | ↗ |
所以当![]() 时,
时,![]() 有极小值,也是最小值,
有极小值,也是最小值,
并且![]() ,
,
综上所述,
当![]() 时,函数
时,函数![]() 不存在最小值;
不存在最小值;
当![]() 时,函数
时,函数![]() 有最小值
有最小值![]() .
.
(Ⅲ)当![]() 时,
时,![]() 与
与![]() 的大小关系等价于
的大小关系等价于![]() 与
与![]() 的大小关系,
的大小关系,
下面比较![]() 与
与![]() 的大小关系:
的大小关系:
令![]() ,则
,则![]() ,
,
当![]() 时,
时,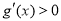 ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,又
上单调递减,又![]() ,
,
故![]() ,即
,即![]() ,故
,故![]() ,所以
,所以![]() .
.

练习册系列答案
相关题目