题目内容
(本小题满分12分)已知数列{an}的前n项和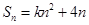 ,
,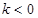 ,且Sn的最大值为8.
,且Sn的最大值为8.
(1)确定常数k的值,并求通项公式an;
(2)求数列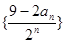 的前n项和Tn。
的前n项和Tn。
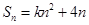 ,
,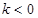 ,且Sn的最大值为8.
,且Sn的最大值为8.(1)确定常数k的值,并求通项公式an;
(2)求数列
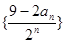 的前n项和Tn。
的前n项和Tn。(1) ;(2)
;(2) 。
。
 ;(2)
;(2) 。
。本试题主要是考查了数列了通项公式与前n项和的关系式的运用。
(1)因为当 时,
时, ,则
,则 ,
, 对于n 令值,得到结论。
对于n 令值,得到结论。
(2)因为 ,因此要运用错位相减法求解数列的和。
,因此要运用错位相减法求解数列的和。
解:(1)当 时,
时, ,则
,则 ,
, ;2分
;2分
当 时,
时,
当 时,
时, 。
。
所以 ……………………6分
……………………6分
(2)∵
 ……(1)
……(1)
 ……(2)
……(2)
(1)-(2):
∴ ………………………12分
………………………12分
(1)因为当
 时,
时, ,则
,则 ,
, 对于n 令值,得到结论。
对于n 令值,得到结论。(2)因为
 ,因此要运用错位相减法求解数列的和。
,因此要运用错位相减法求解数列的和。解:(1)当
 时,
时, ,则
,则 ,
, ;2分
;2分当
 时,
时,
当
 时,
时, 。
。所以
 ……………………6分
……………………6分(2)∵

 ……(1)
……(1) ……(2)
……(2)(1)-(2):

∴
 ………………………12分
………………………12分
练习册系列答案
相关题目
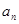 }中,
}中,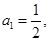 对一切
对一切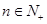 ,点
,点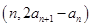 在直线y=x上,
在直线y=x上, 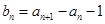 ,求证数列
,求证数列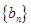 是等比数列,并求通项
是等比数列,并求通项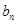 (4分);
(4分);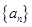 的通项公式
的通项公式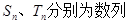
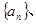
 的前n项和,是否存在常数
的前n项和,是否存在常数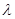 ,使得数列
,使得数列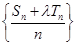 为等差数列?若存在,试求出
为等差数列?若存在,试求出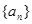 满足
满足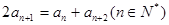 ,它的前
,它的前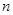 项和为
项和为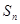 ,且
,且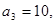
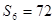 .
.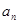 ,
, 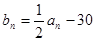 ,求数列
,求数列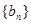 的前
的前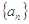 前
前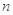 项和为
项和为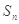 ,
,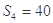 ,
,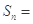 210,
210, 130,则
130,则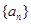 中,
中,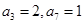 ,且数列
,且数列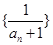 是等差数列,则
是等差数列,则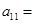 ( )
( )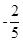
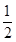
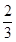
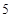
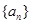 的前n项和为
的前n项和为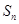 ,点
,点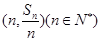 均在函数y=-x+12的图像上.
均在函数y=-x+12的图像上.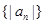 的前n项的和.
的前n项的和.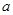 所代表的正整数是
所代表的正整数是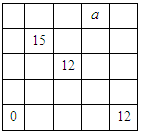
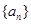 的前n项和为
的前n项和为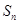 ,若
,若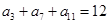 ,则
,则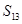 等于( )
等于( ) 的前100项和为( )
的前100项和为( )


