题目内容
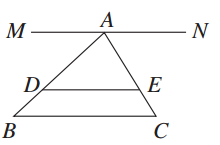
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于点D.过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,EF= ,则线段CD的长为________.
,则线段CD的长为________.

 ,则线段CD的长为________.
,则线段CD的长为________.

如图,由相交弦定理得AF·FB=EF·FC,

∴FC= =2,
=2,
∵FC∥BD,∴ =
= ,BD=
,BD= =
= .
.
又由切割线定理知BD2=DC·DA,
又由DA=4CD知4DC2=BD2= ,∴DC=
,∴DC= .
.
明确相交弦定理、切割线定理等是解题的关键.

∴FC=
 =2,
=2,∵FC∥BD,∴
 =
= ,BD=
,BD= =
= .
.又由切割线定理知BD2=DC·DA,
又由DA=4CD知4DC2=BD2=
 ,∴DC=
,∴DC= .
.明确相交弦定理、切割线定理等是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 是
是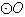 的内接四边形,
的内接四边形,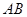 的延长线与
的延长线与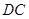 的延长线交于点
的延长线交于点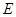 ,且
,且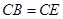 .
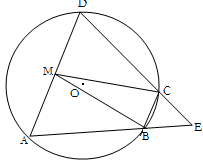
.
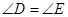 ;
;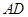 不是
不是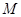 ,且
,且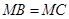 ,证明:
,证明: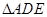 为等边三角形.
为等边三角形.
 ,则
,则 的取值范围是 .
的取值范围是 . 与圆
与圆 相切于
相切于 ,直线
,直线 交圆
交圆 ,
, 两点,
两点, ,垂足为
,垂足为 ,且
,且 的中点,若
的中点,若 ,则
,则 .
.
 CD.则PD=________.
CD.则PD=________.