题目内容
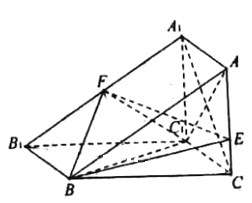
【题目】如图，三棱柱
的侧面
是正方形，平面
平面
，
，
，点
在
上，
，
是
的中点.
（Ⅰ）求证：
平面
；
（Ⅱ）判断平面与平面
是否垂直，直接写出结论，不必说明理由；
（Ⅲ）求二面角
的余弦值.
【答案】（Ⅰ）证明见解析（Ⅱ）平面
平面
（Ⅲ）
【解析】
（Ⅰ）连结
交
于
，因为
为中点，所以
，利用线面平行的判定定理即可证出
（Ⅱ）首先利用面面垂直的判定定理即可得出结论.
（Ⅲ）建立空间直角建立坐标系，分别求出平面
的一个法向量、平面
的一个法向量，利用空间向量的数量积即可求解.
（Ⅰ）如图所示，
连结交于，因为为中点，所以，
又因为
平面
, 
平面,
所以
平面.
（Ⅱ）平面平面.
（Ⅲ）如图建立坐标系，设
，
，
，
设平面的一个法向量为
，则
，
，
令
，则
，同理可得平面的一个法向量为
，
所以
，
因为二面角为锐二面角，
所以求二面角
的余弦值为.
练习册系列答案
相关题目
【题目】一研学实践活动小组利用课余时间，对某公司1月份至5月份销售某种产品的销售量及销售单价进行了调查，月销售单价
（单位：元）和月销售量
（单位：百件）之间的一组数据如下表所示：
月份 | 1 | 2 | 3 | 4 | 5 |
月销售单价 | 1.6 | 1.8 | 2 | 2.2 | 2.4 |
月销售量 | 10 | 8 | 7 | 6 | 4 |
（1）根据1至5月份的数据，求出关于的回归直线方程；
（2）预计在今后的销售中，月销售量与月销售单价仍然服从（1）中的关系，若该种产品的成本是1元/件，那么该产品的月销售单价应定为多少元才能获得最大月利润？（注：利润=销售收入-成本）
（回归直线方程
，其中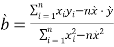
.参考数据：
，
）
