题目内容
【题目】已知函数![]() .
.
(1)若![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(2)若![]() ,且函数
,且函数![]() 的值域为
的值域为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)对函数进行求导得![]() ,再利用导数的几何意义得
,再利用导数的几何意义得![]() ,从而得到关于
,从而得到关于![]() 的方程,解方程即可得到答案;
的方程,解方程即可得到答案;
(2)当![]() 时,
时,![]() ,将函数
,将函数![]() 可化为
可化为![]() ,则
,则![]() ,从而将问题转化为
,从而将问题转化为![]() 有解,再构造函数
有解,再构造函数![]() ,利用导数研究函数的值域,从而得到
,利用导数研究函数的值域,从而得到![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() ,
,
![]() ,
,
由![]() ,
,
得![]() ,
,
即![]() ,
,
解得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,此时直线
,此时直线![]() 恰为切线,故舍去,
恰为切线,故舍去,
所以![]() .
.
(2)当![]() 时,
时,![]() ,设
,设![]() ,
,
设![]() ,则
,则![]() ,
,
故函数![]() 可化为
可化为![]() .
.
由![]() ,可得
,可得
![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,
,
所以![]() 的最小值为
的最小值为![]() ,
,
此时![]() ,函数的
,函数的![]() 的值域为
的值域为![]()
问题转化为当![]() 时,
时,![]() 有解,
有解,
即![]() ,得
,得![]() .
.
设![]() ,则
,则![]() ,
,
故![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,
,
所以![]() 的最小值为
的最小值为![]() ,
,
故![]() 的最小值为
的最小值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】根据国家环保部新修订的《 环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过
的年平均浓度不得超过![]() 微克/立方米,
微克/立方米,![]() 的
的![]() 小时平均浓度不得超过
小时平均浓度不得超过![]() 微克/立方米.我市环保局随机抽取了一居民区
微克/立方米.我市环保局随机抽取了一居民区![]() 年
年![]() 天
天![]() 的
的![]() 小时平均浓度(单位:微克/立方米)的监测数据,数据统计如下表:
小时平均浓度(单位:微克/立方米)的监测数据,数据统计如下表:
组别 |
| 频数(天) | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
(1)这![]() 天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.
天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.

①求图中![]() 的值;
的值;
②求样本平均数,并根据样本估计总体的思想,从![]() 的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由;
的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由;
(2)将频率视为概率,对于![]() 年的某
年的某![]() 天,记这
天,记这![]() 天中该居民区
天中该居民区![]() 的
的![]() 小时平均浓度符合环境空气质量标准的天数为
小时平均浓度符合环境空气质量标准的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】政府工作报告指出,2019年我国深入实施创新驱动发展战略,创新能力和效率进一步提升;2020年要提升科技支撑能力,健全以企业为主体的产学研一体化创新机制,某企业为了提升行业核心竞争力,逐渐加大了科技投入;该企业连续5年来的科技投入x(百万元)与收益y(百万元)的数据统计如下:
科技投入x | 1 | 2 | 3 | 4 | 5 |
收益y | 40 | 50 | 60 | 70 | 90 |
(1)请根据表中数据,建立y关于x的线性回归方程;
(2)按照(1)中模型,已知科技投入8百万元时收益为140百万元,求残差![]() (残差
(残差![]() 真实值-预报值).
真实值-预报值).
参考数据:回归直线方程![]() ,其中
,其中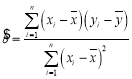 .
.