题目内容
 如图,FD垂直于矩形ABCD所在平面,CE∥DF,∠DEF=90°.
如图,FD垂直于矩形ABCD所在平面,CE∥DF,∠DEF=90°.(Ⅰ)求证:BE∥平面ADF;
(Ⅱ)若矩形ABCD的一个边AB=
| 3 |
| 3 |
| 3 |
分析:(I)过点E作EM∥CD,交FD于M,连接AM,可得四边形CEMD是平行四边形.结合题意得AB∥EM且AB=EM,所以四边形ABEM是平行四边形,得BE∥AM,从而得到BE∥平面ADF;
(II)算出Rt△DEF中DE、DF的长,从而得到Rt△DEF的面积.再以B为顶点、△DEF为底面,得VB-DEF=
S△DEF×BC,用等体积转换得VB-DEF=VF-BDE=
,从而算出BC的长,得当BC=
时,三棱锥F-BDE的体积为
.
(II)算出Rt△DEF中DE、DF的长,从而得到Rt△DEF的面积.再以B为顶点、△DEF为底面,得VB-DEF=
| 1 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
解答:解:(I)过点E作EM∥CD,交FD于M,连接AM
∵CE∥DF,EM∥CD,∴四边形CEMD是平行四边形.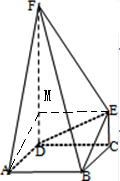
由此可得EM∥CD且EM=CD
∵AB∥CD且AB=CD,∴AB∥EM且AB=EM,
得四边形ABEM是平等四边形,∴BE∥AM,
∵BE?平面ADF,AM?平面ADF,
∴BE∥平面ADF;
(II)由EF=2
,EM=AB=
,得FM=3且∠EFM=30°
由∠DEF=90°,可得FD=4,从而DE=2
∵BC⊥CD,BC⊥DF,CD∩DF=D,∴BC⊥平面CDEF
∴VF-BDE=VB-DEF=
S△DEF×BC
∵S△DEF=
×DE×EF=2
,VF-BDE=
,
∴BC=
=
综上所述,当BC=
时,三棱锥F-BDE的体积为
.
∵CE∥DF,EM∥CD,∴四边形CEMD是平行四边形.

由此可得EM∥CD且EM=CD
∵AB∥CD且AB=CD,∴AB∥EM且AB=EM,
得四边形ABEM是平等四边形,∴BE∥AM,
∵BE?平面ADF,AM?平面ADF,
∴BE∥平面ADF;
(II)由EF=2
| 3 |
| 3 |
由∠DEF=90°,可得FD=4,从而DE=2
∵BC⊥CD,BC⊥DF,CD∩DF=D,∴BC⊥平面CDEF
∴VF-BDE=VB-DEF=
| 1 |
| 3 |
∵S△DEF=
| 1 |
| 2 |
| 3 |
| 3 |
∴BC=
| 3VF-BDE |
| S △DEF |
| 3 |
| 2 |
综上所述,当BC=
| 3 |
| 2 |
| 3 |
点评:本题给出特殊四棱锥,求证线面平行并且求锥体的体积,着重考查了线面平行、垂直的判定与性质和锥体体积公式等知识,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
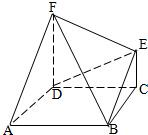 如图,FD垂直于矩形ABCD所在平面,CE∥DF,∠DEF=90°.
如图,FD垂直于矩形ABCD所在平面,CE∥DF,∠DEF=90°.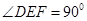 .
.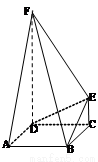
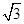 ,EF =
,EF =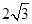 ,则另一边BC的长为何值时,二面角B-EF-D的大小为450?
,则另一边BC的长为何值时,二面角B-EF-D的大小为450?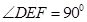 .
. ,EF =
,EF = ,则另一边BC的长为何值时,二面角B-EF-D的大小为450?
,则另一边BC的长为何值时,二面角B-EF-D的大小为450?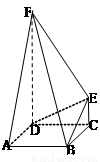
 (2)若矩形ABCD的一个边AB=3, 另一边BC=2
(2)若矩形ABCD的一个边AB=3, 另一边BC=2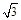 ,EF=2
,EF=2