题目内容
16.已知数列{an}满足2a1+22a2+…+2nan=(2n-1)2n+1+2.(1)求a1及通项公式an;
(2)求证:$\frac{1}{{{a}_{1}}^{2}}$+$\frac{1}{{{a}_{2}}^{2}}$+…+$\frac{1}{{{a}_{n}}^{2}}$<$\frac{1}{4}$.
分析 (1)由2a1=(2-1)22+1+2=6,解得a1=3,同时2nan=(2n-1)2n+1+2-[(2n-3)2n+2]=(4n-2-2n+3)2n,即an=2n+1;
(2)${{a}_{n}}^{2}$=(2n+1)(2n+1)=4n2+4n+1>4n2+4n,所以$\frac{1}{{{a}_{n}}^{2}}$<$\frac{1}{4{n}^{2}+4n}$=$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$,从而$\frac{1}{{{a}_{1}}^{2}}$+$\frac{1}{{{a}_{2}}^{2}}$+…+$\frac{1}{{{a}_{n}}^{2}}$<$\frac{1}{4}(1-\frac{1}{2})$+$\frac{1}{4}(\frac{1}{2}-\frac{1}{3})$+…+$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$<$\frac{1}{4}$.
解答 (1)解:根据题意,得2a1=(2-1)22+1+2=6,解得a1=3,
∵2a1+22a2+…+2n-1an-1=(2n-3)2n+2,
∴2nan=(2n-1)2n+1+2-[(2n-3)2n+2]
=(2n-1)2n+1-(2n-3)2n
=(4n-2-2n+3)2n,
即an=2n+1;
(2)证明:由(1)知${{a}_{n}}^{2}$=(2n+1)(2n+1),
又(2n+1)(2n+1)=4n2+4n+1>4n2+4n,
所以$\frac{1}{{{a}_{n}}^{2}}$<$\frac{1}{4{n}^{2}+4n}$=$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$,
从而$\frac{1}{{{a}_{1}}^{2}}$+$\frac{1}{{{a}_{2}}^{2}}$+…+$\frac{1}{{{a}_{n}}^{2}}$<$\frac{1}{4}(1-\frac{1}{2})$+$\frac{1}{4}(\frac{1}{2}-\frac{1}{3})$+…+$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$
=$\frac{1}{4}(1-\frac{1}{n+1})$<$\frac{1}{4}$.
点评 本题考查了递推式的应用、“裂项求和”,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{20}{21}$ | B. | $\frac{18}{19}$ | C. | $\frac{10}{21}$ | D. | $\frac{9}{19}$ |
| A. | 0 | B. | 1 | C. | $\frac{1}{2}$ | D. | 2 |
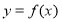 的导函数
的导函数 的图象,则下面判断正确的是( )
的图象,则下面判断正确的是( )
 上
上 是增函数 B.当
是增函数 B.当 时,
时, 取极大值
取极大值 上
上 上
上 ,若
,若 ,则
,则 的范围是 .
的范围是 .